Tonal Rumble: Simultaneous and Successive Bitonality in West Side Story

Andrew Aziz

Abstract

This article offers original listening strategies for two dimensions of bitonality featured in West Side Story, both implied (but not defined) in Bernstein’s writings (1959, 1976): “simultaneous,” or the vertical superimposition of clashing strata, and “successive,” in which non-stratified tonal events generate tonally ambiguous environments, suggesting more than one key. Bernstein’s compositional strategies align with the plot’s trajectory: successive bitonality appears when the gangs stalk each other at a distance (centrally in “Prologue,” “Dance at the Gym Blues,” and “Maria”), with simultaneous bitonality capturing their fateful clash (centrally in “Quintet” and “Tonal Rumble”). Throughout, the analyses apply contemporary theories of tonal transformation (Kaminsky 2004, Rings 2011), scalar dissonance (Martins 2019), and harmonic “divorce” (Temperley 2007, Nobile 2015, De Clercq 2019), amongst others. Finally, I summarize that octatonicism in West Side Story is best contextualized as a processual byproduct of tonal relations, with the seeds sewn in “Prologue.”

View PDF

Keywords and phrases: bitonality, polytonality, tonal ambiguity, Leonard Bernstein, West Side Story

Introduction

The conditions are ripe for tonal clashes in Bernstein’s West Side Story: two opposing forces, the Jets and the Sharks, are fatefully interacting. While many historical, sociopolitical, and even cognitive studies exist, there is a notable absence of close analytical readings of the score.¹ Musical depictions of the gangs’ ongoing struggle include the confluence of acoustically consonant and dissonant intervals (from the opening trichord), the juxtaposition of simple and compound meters, and the superimposition of independent layers. As Elizabeth Wells notes, the compositional environment of the 1950s led Bernstein to employ dissonance both as a structural tool and as a unifying surface detail (2010, 12). The superimposition of different strata, potentially implying multiple tonal centers, has been theorized as “polytonality” (and “bitonality” in the case of two key centers). This article investigates the prevalence of bitonality in Bernstein’s consequential score. 

The article’s primary task is to uncover listening strategies for those passages in West Side Story that offer perplexing, ironic, and even satisfying clashes of sound. In addition, it surveys confounding passages that, despite only projecting one apparent tonal center at a time, may imply more than one. Raymond Knapp describes the distinction:

Broadway’s version of polytonality can involve writing in two or more keys at once, or it can, less jarringly, create an ambiguous tonal environment in which more than one key might serve as a concluding key. (2013, 239)

In the first section, I survey the value of such intuitions based on Bernstein’s archived writings on music. Next, I unpack two distinct forms of bitonality found in West Side Story: “simultaneous,” or the vertical superimposition of strata, and “successive,” in which tonal events generate tonally ambiguous environments, suggesting more than one key. I support my approaches with foundational work on polytonal/polyscalar work by Peter Kaminsky and José Oliveira Martins, perspectives of harmonic divorce in recent popular music studies, and the transformational approach of Steven Rings. I then apply these concepts to chosen numbers in West Side Story, beginning with the “Prologue” and culminating in “Rumble.” A concluding section reflects on the analytical approaches employed (including the treatment of the “octatonic” collection), situating the methodologies within an epistemological context.

Prologue: Bernstein’s Writings 

It is hardly surprising that Bernstein’s acclaimed score is saturated with many evocative sonorities. In his 1959 book, The Joy of Music, in the chapter entitled “Introduction to Modern Music,” he begins with the following:

Here it is a nice, quiet Sunday evening in January, and we are about to listen to some beautiful music. Immediately, this suggests a pattern: low lights, your favorite chair, a glass of beer, a cigarette, those warm bunny slippers- in short, relaxation. And now the music (Example 1). (Bernstein 1959, 305)

This small segment from Igor Stravinsky’s “Song of the Nightingale” was not intended to “shock, or upset the bourgeoisie, or provoke fist fights. It was written to charm, entertain, to be pleasant and touching” (ibid.). It is no accident that Bernstein’s reflexive association with modern music was the juxtaposition of two perfect fifths.² In Bernstein’s sixth Harvard lecture, “Poetry of the Earth,” he elaborates further, crediting Stravinsky as having appeared “like an angel of deliverance, just in time to lead the great rescue operation, the huge project of saving tonality” (1976, 331), doing so by acquiring “some striking new additives—a new dissonantal freedom” (ibid., 338). 

A closer look into his Harvard lectures reveals how Bernstein valued the preservation of tonal elements—such as the perfect fifth—and figures such as Stravinsky, who “saved” tonality. In the fifth lecture, “The Twentieth-Century Crises,” Bernstein describes the landscape as a “river dividing into two forks” (1976, 270). On one side, tonal composers (led by Stravinsky) wished to “extend musical ambiguities” within the confines of the tonal system (ibid.); on the other, nontonal composers (led by Schoenberg) sought to overhaul the tonal system through a “clean break” (ibid., 271). For Bernstein, tonality was preferable to both free atonality and serialism. Free atonality was “extremely difficult for the listener to follow in either form or content” (ibid., 273), and serialism was not based on “innate awareness, on the intuition of tonal relationships” (ibid., 283). Bernstein advocated for Stravinsky’s effort to keep tonality alive and “musical progress on the move” through structural ambiguities (ibid., 337). The ambiguities afforded by serialism were elusive, but those arising from tonal dissonances, such as polytonality, were a natural outgrowth of sustaining tonality.³

Bernstein illustrates his perspective with several famous examples: the C-F$$\sharp$$ “Petrushka” chord, the C-E-E$$\flat$$7 centered ostinati within the Rite’s  “Dance of the Adolescents,” and the G-D duality in Milhaud’s Saudade do Brasil, “Corcovado” (Example 2). Bernstein, describing the Milhaud:

And the point to note is not only that it is bitonal, the left hand in G and the right hand in D, but that it is a Parisian speaking the Brazilian vernacular. Do you see how charming and relaxed bitonality can be? (1976, 361).

These examples engender what I refer to as simultaneous bitonality (or biscalarity), in which multiple tonal centers (or collections) are superimposed. ⁴

Knapp, Wells, and Joseph P. Swain posit that bitonality in West Side Story not only involves passages containing superimposed key strands but also encompasses non-stratified passages that allude to more than one key. Wells connects this notion to Bernstein’s embracing the tonal plan of Wagner’s Prelude to Tristan und Isolde, a centerpiece in the fourth Harvard lecture, “The Delights and Dangers of Ambiguity” (in particular, 1976, 226–237).⁵ The Prelude establishes a close duality with A and C, with an early emphasis on A shifting to C in the final section.⁶ Bernstein also unpacks the “delightful” ambiguity of multiple key centers in the opening of Mahler’s Symphony #5, IV (Example 3).

To Bernstein, ambiguity unlocks the explanation for why audiences “swoon” to the Adagietto, through the withholding of the tonic F for the entirety of the first two measures (“the two notes we hear could turn out to be two-thirds of a whole other triad, namely A minor” (ibid., 199)). Even after the bass finally makes its way to F, a “tug-at-the-heart” in the melody (E) holds the listener in suspense; once it resolves, they “melt away, with the pleasure of fulfillment” (ibid.). As the identity of the triad remains ambiguous, one’s perception of tonic remains fluid; I term the temporal unfolding of different potential tonics successive polytonality. In doing so, I embrace Bernstein’s spirit of tonal ambiguity by tracing passages in West Side Story that summon a similar analytical strategy.

An additional ingredient of Bernstein’s tonal language can be linked back to his undergraduate thesis at Harvard (“The Absorption of Race Elements into American Music”), from which Geoffrey Block demonstrates the continuity of Bernstein’s ideas from youth to maturity (2008, 153). In his dissertation, Lars Helgert traces Bernstein’s usage of a collection containing lowered third, fifth, and seventh scale degrees (2008, 56; 216). Example 4 reproduces a transcription from Bernstein’s Harvard thesis that features this collection.⁷ As we will see, these “blue-note” scale-degree pairings ($$\flat\hat{3}$$/$$\hat{3}$$, $$\flat\hat{5}$$/$$\hat{5}$$, $$\flat\hat{7}$$/$$\hat{7}$$) allow Bernstein to both activate multiple scalar collections with the same tonic (“polyscalarity”). In addition, interpreting blues scale degrees affords a potential dual interpretation of pitches not otherwise found in a diatonic collection. For example, G can flexibly serve as $$\hat{5}$$ in C or $$\flat\hat{7}$$ in A.

Bernstein’s usage of lowered scale degrees engenders the sound of jazz, a topic traced by numerous musicologists. According to Katherine Baber, Bernstein’s “weaving of a tapestry” included all the stylistic choices available to him (2019, 13); in West Side Story, jazz styles converge to confront tensions surrounding race, ethnicity, and gender and to act in response to those tensions (ibid., 156). Matthew Mugmon accounts for Bernstein’s stance that jazz, as an American folk music, became a “natural part of a composer’s vision” (2019, 3). Baber and Nigel Simeone cite Bernstein’s admiration of Milhaud’s La création du monde, which possesses the polytonal and jazz elements that so intrigued him, and that he conducted regularly (Simeone 2013, 319; Baber 2019, 50). In turn, I will discuss how Bernstein draws upon techniques from Milhaud’s and Stravinsky’s works in climactic points of West Side Story.

The scholarly literature by Baber, Block, Simeone, Wells, and others affirm how Bernstein’s primary sources provide explicit guidelines for how he heard music, reflecting his compositional impulses.⁸ Bernstein’s foregrounding of polytonality, dissonance, and ambiguity communicates potential strategies for unpacking an often perplexing surface. The following section codifies my perspectives further, integrating concepts with contemporary scholarship on scalar and transformational theories.

Simultaneous versus Successive Bitonality  

Swain is accurate when he proclaims that “the music of the Prologue is the source of all of Bernstein’s important musical elements” (1990, 213); no source material makes for a more explanatory building block than the opening three notes.⁹ Bernstein himself (chronicled by Wells; 2010, 57) indicated, in a note to a Dutch student in 1969, how the opening three-note “shofar” whistle is the source material for many other numbers, including “Prologue,” “Maria,”  and “Cool”; Helen Smith also cites smaller junctures within “Scherzo” and “Mambo,” as well as “Something’s Coming” and “Cha Cha” (2016, 148). Perhaps a “Petrushka” chord of sorts due to its pitch content and iconic recognition, the opening three-note whistle of G-C-F$$\sharp$$ creates a necessary problem to be solved—its seemingly paradoxical mix of acoustically dissonant and consonant intervals, as well as the pitches’ individual potential for tonal function. 

Such an intervallic study of the opening trichord is carried out by Smith, who traces its various permutations, rhythmic variations, and evolution across the musical.¹⁰ A crucial rhythmic observation is how the “central $$\sharp\hat{4}$$ is shorter than the surrounding notes,” as it typically embellishes the resolution note of $$\hat{5}$$, setting up an appoggiatura. While the three notes of the trichord are typically found in close proximity, one exception where the tritone does not immediately resolve is found in “Gee, Officer Krupke,” the psychological effect of which is discussed in Nagel (2010a).¹¹ Another exception appears in the nontonal context of the “shofar” motive —a perfect fourth + tritone ascending—that realizes the “semitone” as a dissonant major seventh. For example, the C-F-B in “Prologue,” mm. 40–42, cannot be heard as a $$\hat{5}$$-$$\hat{1}$$-$$\sharp\hat{4}$$, as the B lacks any tendency to resolve to C. This iteration of the motive highlights the acoustic incompatibilities of the tritone and the perfect fifth; joined together, they form a clashing major seventh. 

As the pitches of a major seventh are tonally incompatible, the intervals’ existence generates an inherent stratification into multiple layers, setting the stage for simultaneous bitonality.¹²  Simultaneous bitonality occurs most overtly when collections with different tonal centers interact. The two collections may have the same center, however, if they superimpose different chromatic scale degrees or distinct modes (in those instances, bi-“scalarity” or bi-“modality” is a more precise descriptor). Peter Kaminsky analyzes an example of simultaneous bitonality in Ravel’s Violin Sonata, II, “Blues,” reproduced in Example 5. In this work, the keys of A$$\flat$$ major and G major, a major seventh apart, vie for prominence, with Kaminsky arguing that the upper parts eventually become assimilated into the underlying bass line.¹³

Kaminsky’s method examines two dimensions of simultaneous bitonality that manifest throughout West Side Story. First, he separates the music into three strands: 1) the middle-range “treble chords” projecting G major, beginning with the violin and handed off to the piano in m. 12; 2) the bass accompaniment, an A$$\flat$$-E$$\flat$$ perfect fifth; and 3) the upper-range violin melody. By itself, the middle-range G major is unopposed (mm. 1–6), then vies for prominence with the bass’s A$$\flat$$ open fifth in mm. 7–12, resisting assimilation (ibid., 258). Additionally, he considers the scale degree function of pitches through the lenses of the vying keys. Only the treble chord’s B$$\natural$$ is acoustically consonant against the A$$\flat$$-E$$\flat$$; the D and G are incompatible. While the G-F-G of the violin melody more closely aligns with the piano’s treble chords, the F-E$$\flat$$-F begins to veer toward alignment with the bass’s open fifth, especially with the presence of the E$$\flat$$ as $$\hat{5}$$ in A$$\flat$$ major. At the same time, F is a “blue note” $$\flat\hat{7}$$  in G major. The B$$\natural$$/C$$\flat$$ in the violin melody serves as the clinching moment for coherence in both keys, and the tipping point for perceiving A$$\flat$$ major as more prominent. At first, B$$\natural$$ projects $$\hat{3}$$ in G major, before enharmonically transforming into a blue $$\flat\hat{3}$$  of A$$\flat$$ major. 

In contemporary theories of pop-rock music, Trevor de Clercq would classify the Violin Sonata passage as one possessing “harmonic-bass” divorce (similar to his Example 15)¹⁴; the open-fifth A$$\flat$$-E$$\flat$$, akin to a “power chord,” conflicts with the established harmony. The interaction of the violin melody with both the A$$\flat$$-E$$\flat$$ and G-major harmonic layers (depending on what is heard as the referential “harmony”) appeals to what David Temperley (2007) and Drew Nobile (2015) describe as a “melodic-harmonic” divorce. While both the treble chords and bass line insistently project their respective tonics, the violin line initially resists accordance with the A$$\flat$$-E$$\flat$$layer, until gradually “divorcing” the G-major layer altogether and uniting with A$$\flat$$ major in mm. 18–19.¹⁵

To further interpret Bernstein’s stratification of different scalar collections—rather than just chords—we can apply José Oliveira Martins’ theory of polytonal/modal “mismatch” in twentieth-century music.¹⁶ Martins models the interaction of tonally resonant layers, developing an original theoretic construct called “scalar dissonance.” Applied to Milhaud’s “Copacabana” movement of Saudades do Brasil, Martins measures the interactions of different scalar strata. Example 6 reproduces Martins’ score illustrating the competing layers of B major (5-sharp diatonic) and G major (1-sharp diatonic). First, he considers only the pitches used in each hand, the left hand’s G-A-B-C-D against the right hand’s full B-major scale. Through this lens, the hands have only one note in common (B), along with four “mismatches” (G$$\sharp$$/G$$\natural$$, A$$\sharp$$/A$$\natural$$, C$$\sharp$$/C$$\natural$$, D$$\sharp$$/D$$\natural$$), in which diatonic pitches in each collection differ by a semitone. Martins also considers the left hand to imply the remainder of the G-major collection, including E and F$$\sharp$$. The E-F$$\sharp$$s in the right hand synchronizes with both diatonic scales, aligning with the music’s characteristic B-F$$\sharp$$-E motive. 

Martins’ concept of the multiple identities of a particular pitch class participating in bitonality can be applied to the opening three-note motive in West Side Story. In short, a tonal version of the motive does not necessarily possess the scale degree identities of $$\hat{1}$$, $$\sharp\hat{4}$$, and $$\hat{5}$$, as most of the iterations in Smith’s work do. At select points in West Side Story, the semitone  $$\sharp\hat{4}$$ realizes its potential to function as a leading tone $$\hat{7}$$, resolving to a new tonic. As I will discuss in “Something’s Coming,” “Cha Cha,” and “Maria,” Bernstein uses this specific functional ambiguity to cleverly toggle between tonal centers; such reinterpretations fall under the umbrella of successive bitonality. 

While some instances of successive bitonality invite traditional forms of tonal analysis, others (especially “Prologue” and “Jet Song”) call upon a methodology developed by Steven Rings (2011), whose system (an application of David Lewin’s “Generalized Interval System”) of scale degree “qualia” quantifies the functional perception of a pitch class in a given key. Rings represents each individual note as an ordered pair of scale degree and pitch class: (scale degree, pitch class); he also measures the intervallic distance between each individual note, with ordered pairs. The left element is an ordinal number (2^nd, 3^rd, 4^th …), indicating a generic interval between scale degrees, and the right element is the number of semitones ascending or descending (negative integers for descending).

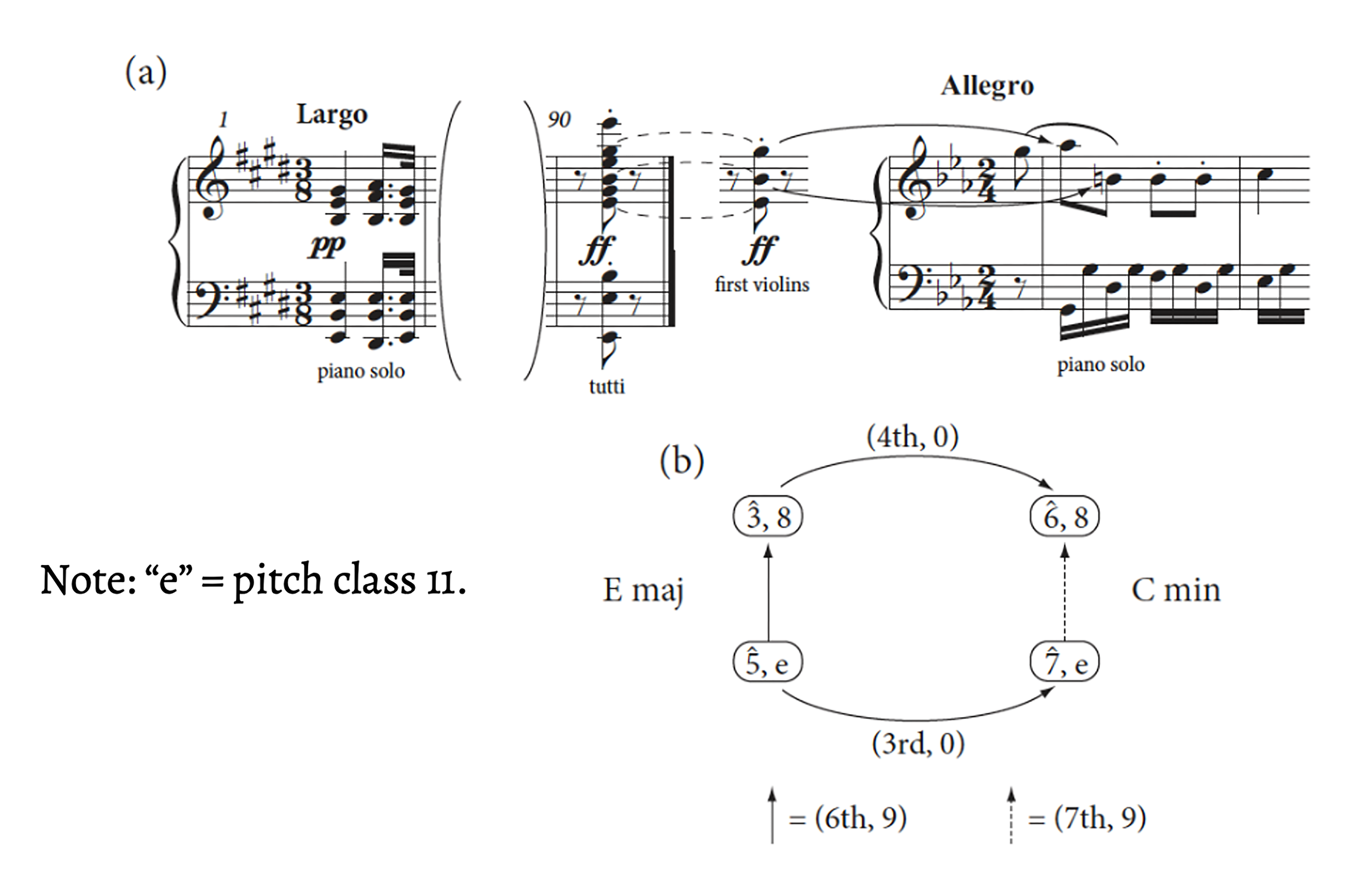
Example 7 illustrates how Rings’ method models perceptual distance traversed between two adjacent keys. Between the second and third movements of Beethoven’s Piano Concerto #3, a modulation from E major and C minor enharmonically recasts B-G$$\sharp$$ as B-A$$\flat$$. Since we are analyzing a pivot chord, the pitch classes do not change (both B’s = 11, and G$$\sharp$$/A$$\flat$$ = 8), yielding pitch distances of 0. The scale degree distances, however, ascend by a third ($$\hat{5}$$ to $$\hat{7}$$) for B and by a fourth ($$\hat{3}$$to $$\hat{6}$$) for G$$\sharp$$/A$$\flat$$, yielding intervallic ordered pairs of (3rd, 0) and (4th, 0), respectively.¹⁷ As I will demonstrate in the next section, such moments of successive polytonality in West Side Story can be understood in similar terms.

Having introduced the primary categories of bitonality, along with several approaches from the scholarly literature, I embark upon a series of vignettes from West Side Story. First, I consider the “Prologue” and adjacent “Jet Song,” the analysis of which contains both successive and simultaneous bitonal events. Throughout both numbers, two keys vie for dual priority. Next, “Dance of the Gym Blues” builds on the “Prologue” in its usage of successive bitonality, while integrating the harmonic scheme from twelve-bar blues. Next, “Something’s Coming,” “Cha-Cha,” and “Maria” all demonstrate successive bitonality, with $$\sharp\hat{4}$$ fluidly tapping into its leading tone potential. If successive bitonality is bitonality by “stealth,” in which two centers exist but are not stratified, such echoes the rival gangs’ state of affairs at the beginning of the “Prologue”: coexistence but avoidance. I employ the word “stealth,” as the presence of successive bitonality is far less overt than simultaneous, and often presented in an intentionally clandestine manner: multiple keys are implied rather than showcased explicitly. As the temperature between the gangs increases, and their interactions more prescient of impending doom, the music—and the analytical approaches—reflect this heightened anxiety. The final two vignettes trace the (mostly) simultaneous bitonality, with maximal dissonance (the “tonal rumble”) in the climactic numbers of “Tonight” Quintet and “Rumble.” 

Successive and Simultaneous Bitonality in “Prologue” / “Jet Song”

The opening of the “Prologue,” when the two rival gangs are stalking each other at a distance, encapsulates Bernstein’s successive bitonality. Swain describes the example:

The opening phrase, for example, begins with a colored C triad and a colored A triad, and ends on a G-sharp triad, also colored. Is the real key C, as the first bass note would suggest, or A, as the second and last would suggest? (2002, 16)

When first introduced to the snapping Jets, Example 8 (analyzed using Rings’ method),  surfaces. Indeed, the music sways between the poles of C and A, and one may, especially upon an initial hearing, toggle back and forth between identifying either as “tonic.” Interpreted as two potential tonic-functioning “major/minor” triads (Example 8a), scale degrees are held constant (0), but the pitches are transposed down three semitones (-3), yielding an intervallic ordered pair of (0, -3). (Hereon, “major/minor” triads will be abbreviated as “M/m.”) Consider, however, an alternative interpretation: what if, after having heard both chords, one analyzes both in A major (Example 8b)? Such a reading imports lowered scale degrees akin to what Bernstein demonstrated in his undergraduate thesis (Example 4), including the first triad containing $$\flat\hat{3}$$, $$\flat\hat{5}$$, and $$\flat\hat{7}$$.¹⁸ Altogether, we can hear both triads in A, with a scale degree transposition down a third and an intervallic ordered pair of (3rd(-), -3).¹⁹

The diminished cadential chord of the phrase sustains the ambiguity of the opening two M/m triads. Within G$$\sharp$$-B-D (with the A$$\sharp$$ for “color”), the G$$\sharp$$ is, spelling-wise, functioning as $$\hat{7}$$ of A, but may also be heard as an enharmonically-veiled A$$\flat$$-B-D, functioning in C.²⁰ The following phrase (mm. 5-8), echoing the same music, reveals the entirety of mm. 1–8 as an antecedent-consequent pair (Example 9), with the G$$\sharp$$ enharmonically respelled as A$$\flat$$.

Suppose that the G$$\sharp$$ at the end of the antecedent is “correctly” spelled as a $$\hat{7}$$ of A (signaling a half cadence), and the consequent’s A$$\flat$$ is also “correct” as a $$\flat\hat{6}$$ of C. If m. 8 implies an authentic cadence of C, A$$\flat$$-B-D substitutes for its purely “dominant” counterpart (G-B-D) in a manner that Richard Bass would characterize as a “shadow” (1988, 199).²¹  One may imagine a hypothetical V that realizes A$$\flat$$’s tendency downward to G (Example 10). 

Following three measures of finger snaps, the alto saxophone and vibraphone perform the hallmark “E4-E5-C$$\sharp$$5-A4-D$$\sharp$$4”—arpeggiating a downward A-major triad + diminished fifth, then sustaining a final D$$\sharp$$. Once the D$$\sharp$$ is articulated, the corresponding orchestra members reiterate mm. 1–3 of the “Prologue” (Example 11). Both triads are recontextualized with the prevailing A-major backdrop (the hearing of Example 8b), and yet, the D$$\sharp$$ is left alone to sonically interact with the two triads. As such, the pitch functions as both $$\flat\hat{3}$$ (in C major), and $$\sharp\hat{4}$$ (in A major). The alto sax and vibraphone reprise the same pitches, though arpeggiating back upward to a C, this time matching the final open octave of m. 8, and a resumption of finger snaps. Altogether, the fluid toggling between C and A continues to capture the essence of successive bitonality.

The music then proceeds to a tonally elusive 12-measure vamp (mm. 22–33). The previous octave leap from E4 to E5 is overshot to F5, arpeggiating via an augmented triad. The treble presents a three-measure pattern, unfolding a diminished triad (B-D-F), while the bass contains an apparent inverted dominant sonority, D7, with a troublesome C$$\sharp$$ (perhaps unsurprising, given that C$$\sharp$$-F$$\sharp$$-C$$\natural$$ is a transposition of the whistle motive). The dissonant grinding of the ostinato layers is marked by a salient compound diminished-octave dissonance between the bass F$$\sharp$$ against rearticulated F$$\natural$$s on the pickups to mm. 22 and 25 (Example 12a). As discussed on p. 7, such a dissonant interval invites stratification that embodies simultaneous bitonality. Kaminsky would argue that such superimpositions act as “catalyst(s) for potential dual organization … using superimpositions as referential sonorities” (2004, 258).

The incompatibility between the treble and bass parts may be interpreted as a “divorce” between the prominent F$$\natural$$ and F$$\sharp$$. In the bigger picture, the bass’s ostinato of D7, featuring the tritone F$$\sharp$$-C, conflicts with the treble’s B-F; consequently, if the bass music were adjusted by a small interval, any stratification would dissolve. Viewed this way, Bass would likely describe the F$$\sharp$$ (and C$$\sharp$$) as an extended shadow, substituting for pitches that work diatonically with the treble. Example 12b and Example 12c offer such substitutions.

In Example 12b, the F$$\sharp$$-C tritone is replaced by G-B, the “C$$\sharp$$-F$$\sharp$$” is shifted up a semitone to “D-G,” and the F4/F5 is heard as $$\hat{4}$$ in a V7 of C major. In Example 12c, the Gs of 12b are replaced with G$$\sharp$$s, and the same Fs are heard as $$\hat{6}$$ of A minor. Instead of either possibility, Bernstein stifles both potential outcomes, choosing a dissonant underpinning.²²

Bernstein’s choice of such a frozen dissonance contributes to the 12-measure vamp’s interthematic function between instances of Example 11’s primary content (mm. 11–18). The hypnotic, wandering nature of the vamp dramatizes the imminent refrains of the content in m. 34 and m. 70, but with a twist: both returns replace mm. 11–18 with confident A major settings, breaking through the bitonal haze. These bursts provide tonal clarity for passages that exhibited uncertainty for all of mm. 1–20. But, A major is not the only breakthrough key in the “Prologue.” The troublesome C$$\sharp$$-F$$\sharp$$ underpinning of the 12-measure vamp, too, finds a reconciliation later in the form of F$$\sharp$$ major (mm. 101–107 and 112–118; mm. 101–104 shown in Example 13). Reconciling the disjunct tonality of the earlier 12-measure vamp, Bernstein changes the treble material to align with the bass. (Perhaps unsurprisingly, the Lydian-shaded B$$\sharp$$ fuses with the F$$\sharp$$ and C$$\sharp$$ as an iteration of the three-note motive!) The F$$\sharp$$-major vamp is then sequenced a whole step to A$$\flat$$ (mm. 122–33) before entering Più mosso centered on B$$\flat$$ (mm. 140–181).

To close off the “Prologue,” we hear three final returns to the primary material: in A over a dominant pedal (mm. 182–191), in B$$\flat$$ over a dominant pedal (mm. 246–56), and, finally, back to C (mm. 262–end). Example 14a displays mm. 262–267, the final exclamation following a “police whistle.” The downward arpeggiation transforms into a vertical cluster, superimposing the C, A, and G$$\sharp$$ triads from Example 8 with their dissonant shadows, F$$\sharp$$, D$$\sharp$$, and C$$\sharp$$, respectively. The vertical manifestations of the “Prologue” arpeggiation are highly reminiscent of the beginning and end of the final number in Part I of Stravinsky’s Rite, “Dance of the Earth,” shown in Example 14b; most noteworthy is how a manifestation of West Side Story’s three-note motive (C-F$$\sharp$$-G) saturates multiple layers in Rite.

The end of the “Prologue” cools down, as it were, using the same music as the beginning and providing a segue into the first vocal number, “Jet Song.” The onset of the “Jet Song” closely mirrors the script of the “Prologue”’s opening: mm. 1–15 appears verbatim, and the 12-measure vamp is reduced to eight and transposed upward by a semitone (mm. 16–23). In m. 24, the “Jet Song” gallop begins in earnest, centered on B$$\flat$$.²³ Similar instances of successive bitonality (involving two keys a minor third apart) underlying the “Prologue” are present during each iteration of the “Jet Song”’s primary verse. Example 15 shows the example sung by Riff, identifying scale degrees in both keys of B$$\flat$$ and G, accompanied by a Rings-style analysis transposed down by step from Example 8. In the “Jet Song” opening, however, B$$\flat$$ major asserts stronger prominence than C initially does in “Prologue,” with every vocal downbeat articulating $$\hat{1}$$ or $$\hat{5}$$, supported by colored  “I” and “V$$^{6}_{5}$$.” Though the presence of G comfortably serves as an added sixth to a B$$\flat$$-major triad, the F$$\sharp$$ in the bass line lurks as a potential leading tone of G.

Viewed through B$$\flat$$ however, the F$$\sharp$$ is enharmonically respelled as G$$\flat$$, $$\flat\hat{6}$$, substituting for F$$\natural$$ (à la the “Prologue”). Maximizing the effect of the bass F$$\sharp$$s, Bernstein strategically places G and F$$\natural$$ in the vocal melody (echoing the F$$\sharp$$/F$$\natural$$ clash of the Prologue’s twelve-measure vamp). After the initial verse of “Jet Song,” Bernstein follows with “Prologue” music in B$$\flat$$ (mm. 67–78) before using the original transposition of the vamp (mm. 80–92) to reinstate the C/A complex. Additional verses appear at m. 137 (an exact transposition of m. 28), m. 164 (in $$^{2}_{4}$$ time), and finally at m. 191. A final exclamation closes off the paired opening numbers, with the upper orchestra performing an arpeggiation of G-E-C-F$$\sharp$$ (in C!).

Successive Bitonality in “The Dance of The Gym Blues”

I will next unpack the complex applications of successive bitonality present in “The Dance at the Gym Blues,” the material of which is initially featured in mm. 116–124 of “Jet Song.” “The Dance of the Gym Blues” imports the minor-third-related tonal pairings established by the “Prologue” (C/A) and “Jet Song” (B$$\flat$$/G). In “Jet Song,” the higher of the two keys (B$$\flat$$) serves in a primary role, and the lower key (G) in a subordinate role, three semitones below; “The Dance of the Gym Blues” resumes a similar framework. This number also elevates two dimensions featured in blues: first, each measure includes triads within a metrically standard twelve-bar blues progression; and second, primary key triads routinely fall on backbeats (usually 4 and sometimes 2), and subordinate key triads on strong beats. 

Table 1 considers an analysis of only mm. 16–28, during which B$$\flat$$ blues is primary, and G subordinate. (The gray-shaded mm. 29–33 is not considered in the reading.) Columns 2-5 list all of the M/m triads on quarter note beats, and Columns 6–7 include all of the harmonies as they would metrically occur within a normative twelve-bar blues. (Column 6 contains the progression in B$$\flat$$ blues, and Column 7 in G.) Harmonies from Columns 6-7, if present in 2-5, appear in bold. A closer look at Column 6 shows that each 12-bar blues harmony (tonic B$$\flat$$, subdominant E$$\flat$$, or dominant F triads) corresponds with the expected location between mm. 17–28, with only one exception: the IV in m. 26. As such, the E$$\flat$$ triad is denoted with a strikethrough. G blues’ subordinate triads (Column 7) only appear in six of the twelve locations: mm. 17–19, m. 21, m. 24, and m. 26; the absent harmonies contain a strikethrough. We can also observe that the primary (B$$\flat$$) key’s tonic triads regularly appear on backbeats, anticipating the subordinate tonics on strong beats. Finally, the last four measures of the blues progression, mm. 25–28, signal a changing of the guard, with B$$\flat$$ blues’ triads shifting exclusively to strong beats (1 and 3) and G blues disappearing entirely.

Measure	Beat 1	Beat 2	Beat 3	Beat 4	12-bar blues in B$$\flat$$	12-bar blues in G
16				B$$\flat$$	(B$$\flat$$, pickup) pickup)
17	G		E$$\flat$$	B$$\flat$$	B$$\flat$$ (1, I)	G (1, I)
18	G		E$$\flat$$	B$$\flat$$	B$$\flat$$ (2, I)	G (2, I)
19	G		E$$\flat$$	B$$\flat$$	B$$\flat$$ (3, I)	G (3, I)
20	F	B$$\flat$$	F	E$$\flat$$	B$$\flat$$ (4, I)	G (4, I)
21	C		A$$\flat$$	E$$\flat$$	E$$\flat$$ (5, IV)	C (5, IV)
22	A$$\flat$$	E$$\flat$$	A$$\flat$$	E$$\flat$$	E$$\flat$$ (6, IV)	C (6, IV)
23	B$$\flat$$		G	E$$\flat$$	B$$\flat$$ (7, I)	G (7, I)
24	D$$\flat$$	B$$\flat$$	D$$\flat$$	A$$\flat$$	B$$\flat$$ (8, I)	G (8, I)
25	F		D$$\flat$$	E$$\flat$$	F (9, V)	D (9, V)
26	C		A$$\flat$$	D$$\flat$$	E$$\flat$$ (5, IV)	C (10, IV)
27	B$$\flat$$	D$$\flat$$	B$$\flat$$	D$$\flat$$	B$$\flat$$ (11, I)	G (11, I)
28	B$$\flat$$	D$$\flat$$	B$$\flat$$	D$$\flat$$	B$$\flat$$ (12, I)	G (12, I)
29	G$$\flat$$	E$$\flat$$	G$$\flat$$	E$$\flat$$
30	D$$\flat$$	B$$\flat$$	D$$\flat$$	B$$\flat$$
31	A$$\flat$$
32	A$$\flat$$
33	D$$\flat$$

Table 2 reads a primary-subordinate 12-bar blues progression of D$$\flat$$ /B$$\flat$$ that emerges as the initial B$$\flat$$/G progression wanes. The itineraries of both tables’ 12-bar formulae dovetail between mm. 24–28, setting up a competition for prominence between D$$\flat$$ and B$$\flat$$ as primary, culminating in the vamping tonal “battle” in mm. 27–28 (Example 16). In Table 1, mm. 27–28 mark the ending of B$$\flat$$’s role as primary; Table 2 reads a continuation of its subordinate role. Alterations of the 12-bar model first appear in m. 28, which—still engrossed in the tonic battle—delays IV until m. 29; then, m. 30 truncates what should be two bars of tonic before giving way to an emphatic authentic cadence in mm. 31–33.

Measure	Beat 1	Beat 2	Beat 3	Beat 4	12-bar blues in D$$\flat$$	12-bar blues in B$$\flat$$
16				B$$\flat$$
17	G		E$$\flat$$	B$$\flat$$
18	G		E$$\flat$$	B$$\flat$$
19	G		E$$\flat$$	B$$\flat$$
20	F	B$$\flat$$	F	E$$\flat$$
21	C		A$$\flat$$	E$$\flat$$
22	A$$\flat$$	E$$\flat$$	A$$\flat$$	E$$\flat$$
23	B$$\flat$$		G	E$$\flat$$
24	D$$\flat$$	B$$\flat$$	D$$\flat$$	A$$\flat$$	D$$\flat$$ (1, I)	B$$\flat$$ (1, I)
25	F		D$$\flat$$	E$$\flat$$	D$$\flat$$ (2, I)	B$$\flat$$ (2, I)
26	C		A$$\flat$$	D$$\flat$$	D$$\flat$$ (3, I)	B$$\flat$$ (3, I)
27	B$$\flat$$	D$$\flat$$	B$$\flat$$	D$$\flat$$	D$$\flat$$ (4, I)	B$$\flat$$ (4, I)
28	B$$\flat$$	D$$\flat$$	B$$\flat$$	D$$\flat$$	G$$\flat$$ (5, IV) (D$$\flat$$ instead!)	E$$\flat$$ (5, IV) (B$$\flat$$ instead!)
29	G$$\flat$$	E$$\flat$$	G$$\flat$$	E$$\flat$$	G$$\flat$$ (6, IV)	E$$\flat$$ (6, IV)
30	D$$\flat$$	B$$\flat$$	D$$\flat$$	B$$\flat$$	D$$\flat$$ (7/8, I), only 1 bar!	B$$\flat$$ (7/8, I), only 1 bar!
31	A$$\flat$$				A$$\flat$$ (9)	F (9)
32	A$$\flat$$				A$$\flat$$ (10)	F (10)
33	D$$\flat$$				D$$\flat$$ (11–12)	B$$\flat$$ (11–12)

$${\Large\mathbf{\sharp}}$$$${\Large\mathbf{\hat{4}}\text{ }}$$ as Leading Tone: “Something’s Coming” / “Cha-Cha” / “Maria”

The successive bitonality of keys a minor third apart is a feature of both “Prologue”/”Jet Song” and “The Dance of the Gym Blues.” I now return to another instance of successive bitonality inherent to the initial three-note whistle, first discussed on p. 7. I feature (à la Smith) a permutation in which two of the three notes form an adjacent semitone; in “Maria,” the result is an appoggiatura figure, interpreted as $$\sharp\hat{4}$$, which naturally resolves upward to $$\hat{5}$$. Such appoggiaturas were not yet prominent in “Prologue,” however, as $$\sharp\hat{4}$$ remained separated from its resolution partner. For example, in m. 12 of the “Prologue” (Example 11), E-(C$$\sharp$$)-A-D$$\sharp$$ arpeggiates a $$\hat{5}$$-$$\hat{3}$$-$$\hat{1}$$-$$\sharp\hat{4}$$ scale-degree pattern, with the E and D$$\sharp$$ a compound semitone apart, and the D$$\sharp$$ left “hanging.” The arpeggiation is eventually verticalized in Example 14a, highlighting the acoustic dissonance of this interval. 

The “Maria” ascending semitonal gesture first gains prominence in “Something’s Coming”; one may interpret the attractive force of $$\sharp\hat{4}$$ to $$\hat{5}$$ to Tony’s premonition of becoming acquainted with Maria. The initial $$\sharp\hat{4}$$ has the potential for converting its chromatic embellishing function to that of a new leading tone, activating the dominant-related key. The initial measures of “Something Coming” deliver D-G$$\sharp$$-A in Tony’s melody (“Who knows?”) and the treble accompaniment (as shown in Example 17), with an apparent scale degree function of $$\hat{1}$$-$$\sharp\hat{4}$$-$$\hat{5}$$. The harmonic underpinning, however, is looping consecutive perfect fourths (D-A-E).

One possible interpretation is that the E, $$\hat{2}$$ of D major, is really a shadow, substituting for tonic D; such a reading, however, underplays the E’s role in stratifying the bass from the treble layer. Though E does not generate the acoustically intervallic clash of, say, a major seventh (à la Example 12a), it is unlikely to function as $$\hat{2}$$ in the third beat of a galloping $$^{3}_{4}$$ meter. Instead, I posit an interpretation of tonal stratification, in which the bass layer stealthily implies A major, with E as $$\hat{5}$$. This reading of simultaneous bitonality also activates the leading tone potential of the G$$\sharp$$ in the lyric “knows?” While there is no full realization of A major, the stage is nevertheless set for future conversions of $$\sharp\hat{4}$$ to leading tones in a dominant-related key.

A transposition of similar music in C major, this time in $$^{2}_{4}$$ time, removes the destabilizing force, focusing on C-G in the bass. The accompaniment pattern of the C-major section, with sustained F$$\sharp$$s between tonic triads (m. 86, m. 89), stretches the role of F$$\sharp$$ beyond that of a vocal appoggiatura (Example 18). In a flash, the music abruptly climbs from C major back to D, with two moves that instantaneously activate the leading tone function of $$\sharp\hat{4}$$: first, from C to G, and then G to D. The music of mm. 85–90, first appearing in mm. 62–67, initially resolved m. 67’s V⁷/IV to IV in m. 68. Measures 85–90 do not follow suit, spurning the resolution to IV and instead “resolving” the vocal’s B$$\flat$$ to B$$\natural$$, supported by a G-major triad with an added sixth (m. 91). The what-would-have-been $$\sharp\hat{4}$$ acquires leading tone function, retrospectively turning m. 87’s tonic chord into a pivot between C and G major. The same formula immediately unfolds in m. 94, with $$\sharp\hat{4}$$ achieving leading tone status (C$$\sharp$$ resolving to D in m. 98) and m. 91 serving as a retrospective pivot. The passage recycles once more (mm. 140–53) before reverting to the original $$^{3}_{4}$$ vamp (m. 169). 

The ambiguous quality of $$\sharp\hat{4}$$ as a potential leading tone in the dominant key resumes in “Cha-Cha.” In this number, C$$\sharp$$, $$\sharp\hat{4}$$ in G major, hints at the nearby dominant key of D. The long-anticipated number, “Maria,” imports “Cha-Cha” music; measures 211–216 of “Cha-Cha” correspond directly to mm. 9–14 of “Maria,” then 219–29 of the former to 15–25 of the latter. Almost all of “Maria’s” music is found in “Cha-Cha,” except for three additional, crucial measures in “Maria” addressed below. The activation of $$\sharp\hat{4}$$ as a leading tone in the dominant key spurs segments of successive bitonality between the keys of E$$\flat$$ and B$$\flat$$ major.²⁴ Example 19 illustrates a harmonic analysis of “Maria”’s mm. 9–28;  the presence of the A$$\natural$$ in mm. 9–12 positions the music to comfortably coexist in E$$\flat$$ (I and V) and B$$\flat$$major (IV and I). Upon the inclusion of A$$\flat$$, pure E$$\flat$$ finally appears with an apparent imperfect authentic cadence in mm. 13–14 (ii⁷ -V⁷ -I⁷). Mm. 15–16 reestablish bitonality with a restatement of mm. 9–10, before abruptly straying from E$$\flat$$ major via D-minor triads (m. 17, m. 20). The presence of D minor in m. 20—a non-cadential iii in B$$\flat$$ major—undermines the interpretation of mm. 9–14 and mm. 15–20 as a parallel period structure. Instead, m. 14’s cadential event in E$$\flat$$ major is demoted to one of “limited cadential scope” (Caplin 2004, 89). In retrospect, mm.’s 9–14 and 15–20 together form a presentation of a brewing compound sentence.

Following m. 20, we are temporarily vaulted back to E$$\flat$$ major via an A$$\flat$$-major triad in mm. 21–22 (exclaiming “Ma-ri-a!”), only for B$$\flat$$ to be immediately resummoned in m. 23. Then, a twist: B$$\flat$$-minor (mixture) + F-major chords in mm. 24–25 (“so soft and it’s almost like praying”) signal a seemingly terminal half-cadential event in B$$\flat$$ major. At this juncture, the correspondence with “Cha-Cha” ends. Instead of ending on m. 25’s dominant, “Maria” redirects back to the key of E$$\flat$$ major in mm. 26–28, vanquishing the centricity of B$$\flat$$ (at least for now); these bars provide tonal closure that purposefully eludes “Cha-Cha.”  The remainder of “Maria” echoes the same script, with mm. 29–47 supplying a written-out repeat of mm. 9–28.

Tonal Rumble in the “Tonight” Quintet

Over the remainder of the paper, I focus on the two climactic numbers in West Side Story: the “Tonight” Quintet (hereon, “Quintet”) and “Rumble.” Before delving into the “Quintet,” it is crucial to establish a few essentials of “Tonight.”

First sung by Maria in the long-awaited B$$\flat$$ major, the initial verse comprises four eight-measure phrases. Three of the phrases begin with an alternation between the tonic and $$\sharp\hat{4}$$–inflected neighbor chords, channeling the recently completed “Maria” (Example 20). The second phrase temporarily shifts a minor third to D$$\flat$$—continuing to reinforce the minor-third tonal complex—but veers back to a minor-inflected B$$\flat$$ zone for phrase three, until reprising the opening material for phrase four. After all four phrases are complete, the $$\hat{1}$$ and $$\sharp\hat{4}$$ of B$$\flat$$ are reinterpreted as $$\flat\hat{2}$$  and $$\hat{5}$$, embracing a modulation down by semitone to A major (also discussed by Swain 1990, 211). After reprising all four phrases in A major, the same modulatory scheme sinks the music downward to A$$\flat$$ major. 

In one fell swoop, the “Quintet” vanquishes the tritone-filled and minor-third-infused sound worlds with a piercing augmented sonority and haunting ostinato. In Spielberg’s 2021 version of West Side Story, the onset of the sonority is depicted in a fitting dramatic fashion. As a roomful of police officers ponder strategies for thwarting the planned rumble, the ostinato of the “Quintet” fades in. Then, the sonority strikes just as the Jets’ tools collapse onto the ground. The “tonal rumble” is on, as is the scene of the most salient instances of simultaneous bitonality.²⁵ Several commentators have noted layers of tension in the scene. Swain, who also discusses the intersection of keys in this scene, states: “By dramatizing this inextricable intertwining of love and hate in consistent musical motives and symbols, the quintet summarizes the progress of the tragedy just before the fatal moment.” (ibid., 234). Wilfrid Mellers describes the interaction of the feuding gangs in the scene as follows: “Like two countries at war, they both believe they’re right, and they both believe they will triumph” (2001, 88). Julie Nagel characterizes the polyphony as providing “an aural analogue of the characters’ verbal expression of latent and manifest motivations, drives and defenses, preoedipal and oedipal themes, complex relationships, and affects including love, hate, prejudice, jealousy, and revenge” (2010b, 657). By examining the simultaneous bitonality that these passages exude, my analysis to follow will deepen our musical understanding of the tensions described by these authors.

The ostinato’s bass (E-F$$\sharp$$-G$$\sharp$$) strikes with opposing C-E dyads in the upper parts, supplying the initial augmented triad in m. 1 (Example 21). The apparent A-minor underpinning of E-F$$\sharp$$-G$$\sharp$$ initially suggests C-E as a pairing of $$\hat{3}$$-$$\hat{5}$$. The schism that gives rise to simultaneous bitonality is circled in m. 2: the troublesome dissonance between G$$\sharp$$ and G$$\natural$$ upon entrance of the middle layer’s parallel thirds. This characteristic dissonance in the “Quintet” invokes two companion examples: Stravinsky’s “The Ritual of Two Rivals Tribes” from Rite and the opening of Milhaud’s La création du monde.

Unsurprisingly, Bernstein sets his “Quintet,” with two rival gangs about to fatally clash, in a similar vein as Stravinsky’s Rite. Example 22 supplies two musical excerpts from “The Ritual of Two Rivals Tribes”: mm. 1–4 and mm. 59–64. Centering on mm. 3–4  in Example 22a, Stravinsky’s four-hand transcription yields consecutive white-note diatonic thirds in Piano 1, competing against a very chromatic version an octave below in Piano 2.

Piano 2’s pitch choices are not random, however, as the qualities of the thirds are always inverted (major becomes minor, and vice versa). When Piano 1 plays a major third (e.g., F-A), the lower note is raised in Piano 2 (e.g., F$$\sharp$$-A); likewise, when Piano 1 plays a minor third, the upper note is raised in Piano 2. Consequently, there is always a diminished octave simultaneity between the two parts. Later in “Tribes” (Example 22b), starting in m. 61, the left-hand parts of both pianos project a G$$\sharp$$ against the right hands’ G$$\natural$$s within the white-note diatonic, as in the “Quintet.” Neither of the Stravinsky passages declares any specific tonal universe, as the white-note diatonic layer’s claim to “C major” is fragile at best. 

Expressing a very different mood, we see a similar construction within another of Bernstein’s favored compositions, Milhaud’s La création du monde, from the outset (Example 23). A murmuring bass line hovers between D and F$$\sharp$$, and middle-register diatonic thirds (1$$\flat$$) clash between the F$$\sharp$$s in the bass and middle register’s F$$\natural$$s. Unlike in Rite, however, La création projects a clear D center in both layers, while the F$$\natural$$/F$$\sharp$$ superimposition (perhaps a major $$\hat{3}$$ against a “blue” $$\flat\hat{3}$$) provides a dissonant clash.

Prior to its appearance in the “Quintet,” West Side Story prominently features scalar dissonance in the opening section of “America” (Example 24a). The section features three strata that place B$$\flat$$ and B$$\natural$$ in opposition: a middle-register’s floating triplets in G natural minor (or C dorian), a vocal soloist arpeggiating G-major triads multiple times, and the bass line’s open C-G fifths (asserting a center of C). Example 24b reveals three possible hearings: 

1. the two upper layers engage separately from the bass (a “harmonic-bass” divorce);
2.  the voice remains independent from the middle layer and bass (a “melodic-harmonic” divorce); or 
3. the bass assimilates both upper layers.

In Example 24b, mismatches are indicated in bold, with implied pitches in parentheses.

In Case 1 (“harmonic-bass” divorce), the two upper layers together engage G-centered collections: G natural minor in the middle layer and G major (omitting E and F$$\sharp$$) in the vocal layer. While this magnifies the $$\hat{3}$$ mismatch of B$$\flat$$/B$$\natural$$, the absence of $$\hat{6}$$ or $$\hat{7}$$ limits any further explicit scalar dissonance. The bass’s C-G, however, asserts a different tonal center of C, either dorian or melodic minor, filtered through either harmonic layer. Case 2 (“melodic-harmonic” divorce) combines the now C-centered middle and bass layers, pitting them against the G-centered vocal line. The bass engulfs the middle layer, together implying C dorian. The B$$\natural$$ in the voice explicitly clashes with the B$$\flat$$ in the middle layer, while the E$$\flat$$-F in the middle layer implicitly clashes with the voice’s implied E-F$$\sharp$$. Finally, total bass assimilation (Case 3) asserts an entirely C-centered framework in all three layers, including C melodic minor in the vocal line. As a result, E$$\flat$$-F is implied in all layers, eliminating any scalar dissonance.

The “Quintet” presents a related scenario: the bass line ostinato $$\hat{5}$$, $$\hat{6}$$, and $$\hat{7}$$ imposes an implied tonal center of A melodic minor (Example 25). The vocal line (featuring Riff, Bernando, and eventually Anita) never showcases G$$\natural$$, cleanly assimilating into the bass’s implied A center. The instrumental’s white-note diatonic thirds, however, with their insistent G$$\natural$$s, continue to assert their independence as G-major triads and eventually G M/m sevenths (m. 13), implying dominants of C. In the first two beats of m. 13, however, G$$\natural$$ is absent from the middle layer, allowing for bass assimilation and implying V7  and  V9 sonorities. The vocal F$$\natural$$, however, notably clashes with the F$$\sharp$$’s melodic minor underpinning (circled in m. 13).  

Starting in m. 37 (Example 26a), all parts commit to A centricity in a jazzy section (even acknowledged by the lyrics!), with a blue $$\flat\hat{7}$$ suggesting mixolydian in the vocal line. Conspicuously, F$$\natural$$ in the bass creates the same major third span as in the “Quintet” and generates the augmented sonority F$$\natural$$-A-C$$\sharp$$ (first heard as early as m. 21 of the “Prologue”). In m. 38 (circled), the F$$\natural$$ also creates audible clashes with the vocal’s F$$\sharp$$, inverting the relationship from m. 13. One can also imagine a version in which the F$$\natural$$s were instead Es akin to the recomposition of m. 8 in  “Prologue” (Example 10). Instead, the sinister F$$\natural$$s continue to signal the terror that the rival gangs will soon inflict upon each other.

The “Quintet” then shifts to Tony’s rendition of “Tonight” (A major), followed by a complete reprise of the “Quintet’s” opening, transposed up a minor third (C minor). In Maria’s complementary rendition of “Tonight,” the same pattern in Example 26a (“We’re going to rock it tonight”) is transposed at various pitch levels to fit with “Tonight’s” accompaniment (e.g., mm.’s 118, 120, 124, 126, 128), each time assuming the same scale degree pattern as the original (Example 26b). In mm. 130–132 (Example 27), however, Bernardo and Anita sing two altered versions. Bernardo’s is an augmentation (mm. 130–131), with scale degrees adjusted to synchronize with the underlying accompaniment. Most notably, the previously perfect-fourth leaps ($$\hat{5}$$ to $$\hat{1}$$) become perfect-fifth leaps ($$\hat{6}$$ to $$\hat{3}$$). Anita’s version (B-E-D-E-B-D-C$$\sharp$$) is a direct transposition, but the Es—instead of serving as $$\hat{1}$$—appear as upper neighbors to D, with the final C$$\sharp$$ a fitting augmented fourth above the root (G).

In the waning moments of the number (Example 28), the white-note thirds finally undergo their own diatonic transformation, infusing an F$$\sharp$$ into the white-note collection.²⁶ By importing a sharp, the passage spotlights the $$\sharp\hat{4}$$ previously missing from the earlier “Quintet” music but central to the “Tonight” music—the ultimate fusion of forces.

Tonal Rumble in “Rumble”

The “Rumble” is a culmination of tonal hostilities bubbling throughout the musical, featuring distortions of earlier numbers—most centrally “Prologue” and “America.” In perhaps the most “atonal” sounding number, the bass supplies brutal Stravinskyian “hits” of a C-F$$\sharp$$ tritone; above, the triadic pattern draws upon “Prologue” material, as shown in Example 29.²⁷ Echoing the relationship of the tritone, the initial F$$\sharp$$ substitutes for the “Prologue”’s initial C. After repeating F$$\sharp$$, “Rumble”’s shift to A in m. 5 inverts the relationship—transposing up three semitones to A—from the “Prologue,” which shifted down three semitones. After returning to F$$\sharp$$, the climb from F$$\sharp$$ up to C$$\sharp$$ mirrors the earlier downward move from C to G$$\sharp$$. An essential distinction: Bernstein climbs the perfect fifth (+7), rather than echoing the “Prologue’s” descending diminished fourth (-4). E$$\sharp$$s are sustained in the highest register when Riff and Bernando draw blades. Underneath the E$$\sharp$$, Bernstein brings back “America” in the most dystopic way: C$$\sharp$$ triads (mm. 7–10) are conjoined with alternating Cs and Gs to form simultaneous bitonality. This distorted transformation of “America” provides a musical foil to the gleeful exclamation of the earlier number.

After the mirrored “Prologue” is repeated, an extended dystopic “America” repeats up a whole step: D vs. E$$\flat$$ (mm. 17–33). Throughout West Side Story, a certain inevitability about the fate of E$$\flat$$ has lingered. As early as the “Prologue,” though C, A, and F$$\sharp$$ were represented explicitly, the fourth element of the minor-third cycle, E$$\flat$$, was largely absent from the musical. That is, until “Maria” and her altogether familiar motive; even then, a stable E$$\flat$$ was conscientiously avoided. As discussed by Posen (2016, 52), E$$\flat$$ is explored generously amongst a flurry of minor-third-related transpositions, culminating in a “Rumble Chord” (as termed by Posen; ibid., 68) that coincides with an off-stage siren. If “Maria” graced us with an E$$\flat$$-major triad with its characteristic A$$\natural$$, the “Rumble Chord” is the depths of despair: E$$\flat$$-minor, also with A$$\natural$$. (After its impact in “Rumble,” the “Rumble Chord” reappears, fittingly, at the end of “Procession and Nightmare.”) The opening “Prologue” music finds a few last gasps in “Rumble”: twice during mm. 38–46, and mm. 113–116.

Example 30 juxtaposes mm. 1–4 of “Prologue” with the corresponding measures in “Rumble.” The top voice in “Rumble” forms E$$\flat$$-C-E$$\flat$$-B$$\flat$$, a direct transposition of “Prologue”’s G-E-G-D. Against the top voice are diminished octave shadows, akin to the F$$\sharp$$/F$$\natural$$ verticality found in “Prologue”’s mm. 20–27 and throughout various passages of the “Quintet.”

A closer look, however, reveals an even closer relationship than transposition alone. In fact, the diminished octaves in “Rumble” are identical in pitch class to the semitones found in the blues-inflected major/minor triads in “Prologue” but now widened for “Rumble.” The bass part features tritone “hit” chords, as the opening of the “Rumble,” but echoes the same bass line as “Prologue” with one exception: G$$\sharp$$ is now G$$\natural$$. The G$$\natural$$ clarifies a relationship suggested but not realized in the “Prologue” itself: tonic (C) and dominant (G) scale degrees—another flash of functional tonality in the most dissonant of universes; implied only via shadow (see Example 10) until “Rumble,” $$\hat{5}$$ is, at last, finally heard.

Conclusion: West Side Story and the Octatonic; and “Finale”

Readers of this essay will note the conspicuous absence of “octatonic” as an analytical descriptor for much of West Side Story’s pitch organization, key schemes, and transposition patterns. As Posen discusses, the “Rumble,” in particular, engages the octatonic collection. Both the (016) set class (3-5) and all major and minor triads (3-11), when transposed by 3, 6, or 9 semitones, will remain in the same octatonic transposition (2016, 51–52). Across the musical, Bernstein’s tonal ambiguity often engages keys a minor third apart, showcasing tonal centers C and A. By extension, F$$\sharp$$ and E$$\flat$$ exist in the same minor-third—and thus octatonic—orbit. 

Arguments against asserting octatonicism as a primary analytical lens are outlined by Tymoczko (2002, 85). Most applicable in West Side Story is the notion that, since its building blocks are octatonic subsets, the result is “octatonic music,” and the collection is analytically a priori. Centrally, one is often faced with the classic paradox of perception for moments like the “Petrushka” chord, mm. 70–72 of Ravel’s Jeux d’eau, or Example 1 (and as we will see, at the end of the “Finale”): are they best explained by the application of a singular collection, or instead through the interaction of competing musical layers? Opponents of polytonality as an analytical construct (see fn. 12) are inclined to hear such phenomena as a musical alloy: the combination of layers becomes homogenized into a single structure. Support for a “polytonal” or “polyscalar” analytical bent calls for continued attention toward the interaction of constituent elements. 

My analyses of octatonic passages in West Side Story showcase successive and simultaneous bitonality from a “bottom-up” view; recognition of “octatonic” materials is an a posteriori observation. In the “Prologue,” tonal centers C and A earn the bulk of our attention, and the presence of G$$\sharp$$/A$$\flat$$  only reinforces this tension. Even once an “authentic cadence” in C provides confirmation, A major establishes itself as the “priority” throughout; yet, F$$\sharp$$ breaks through, and the entire number ends with proclamations of C. A similar dual complex is found in the “Jet Song,” where the B$$\flat$$is heard as primary, with G lurking, akin to the “Prologue.” “Dance at the Gym Blues” takes the dual priority concept to an even higher plane: first juxtaposing B$$\flat$$ and G, with B$$\flat$$ as priority, then fluidly transforming into a D$$\flat$$/B$$\flat$$ duality, with D$$\flat$$ as priority. The “Quintet,” in a synthetic fashion, forms simultaneous bitonality, stacking the centers of C and A that the “Prologue” previously exhibited in a successive manner. Correspondences with the octatonic collection, where they appear, are a resultant byproduct of juxtapositions sculpted by the music. 

The “rumble” movements of “Quintet” and “Rumble” exemplify simultaneous bitonality, the seeds of which are sown as early as “Prologue” and the opening scene of “America.” These acoustic fractures further ingrain the natural split between the rival gangs. In many cases, the interval of a diminished octave creates a sense of tonal bifurcation, as two keys a semitone apart are tonally incompatible. Even altering a single pitch establishes a sense of independence between layers, creating a sensation of listening to two conversations simultaneously. As Martins concludes in his 2019 essay: focusing on scalar dissonance reframes the discussion to be “less about the specification of identities” and “more about empirical effects” (83). 

Such effects appear in the “Finale,” capturing the essence of ultimate tonal disrepair (Example 31). The music is separated into three octaves of strata, with the lowest serving as a drone; the upper two strata have interlocking chords one octave apart. While mm. 15–18 project E- and F$$\sharp$$-major triads (a familiar $$\sharp\hat{4}$$ universe), mm. 19–22 insert more insidious chromaticism against an E pedal. In m. 19, the F$$\sharp$$ triad shifts up a semitone to G$$\natural$$ major (a “bluesy” chord against the pedal), then “correcting” itself back to E. In mm. 20–21, three consecutive vertically mismatched octaves tug at one’s heartstrings: E/E$$\sharp$$, C$$\sharp$$/C$$\natural$$, and A$$\sharp$$/A$$\natural$$. The top line then soars to an F$$\sharp$$, joined by F$$\sharp$$’s underlying pedal point. F$$\sharp$$ projects $$\hat{5}$$, with a canonic B-major reminiscence of “Somewhere,” suggesting more optimistic days ahead. Then, with F$$\sharp$$ holding firm in the lowest reaches, B major inches upward to C major, solidifying our reality: F$$\sharp$$ and C—just as the Jets and Sharks—are incompatibly stratified.

---

References

Amos, Laura Christine. 2007. “An Examination of 1920s Parisian Polytonality: Milhaud’s Ballet La création du monde.” Ph.D. diss., University of Texas. 

Baber, Katherine. 2019. Leonard Bernstein and the Language of Jazz. Urbana: University of Illinois Press. 

Bailey, Robert. 1985. Prelude and Transfiguration from “Tristan und Isolde,” Richard Wagner. New York: Norton.

BaileyShea, Matthew. 2007. “The Hexatonic and the Double Tonic: Wolf’s ‘Christmas Rose.’” Journal of Music Theory 51 (2): 187–210.

Bass, Richard. 1988. “Prokofiev’s Technique of Chromatic Displacement.” Music Analysis 7(2): 197–214. 

Baur, Steven. 1999. “Ravel’s ‘Russian’ Period: Octatonicism in His Early Works, 1893-1908.” Journal of the American Musicological Society 52 (3): 531–592. 

Berger, Arthur. 1963. “Problems of Pitch Organization in Stravinsky.” Perspectives of New Music 2 (1): 11–42. 

Bergeron-Dumaine, Holly. 2018. “Differentiation of Concurrent Musical Strata.” M.A. Thesis, McGill University.

Bernstein, Leonard. 1959. “Introduction to Modern Music.” In The Joy of Music, 333–403. New York: Simon and Schuster.

_____. 1976. The Unanswered Question, Six Talks at Harvard. Cambridge: Harvard University Press.

Bernstein, Leonard, and Stephen Sondheim. 1957. West Side Story (Piano Vocal). Music Theatre International.

Block, Geoffrey. 2008. “Bernstein’s Senior Thesis at Harvard: The Roots of a Lifelong Search to Discover an American Identity.” College Music Symposium 48: 52–68.

Caplin, William. 2004. “The Classical Cadence, Conceptions and Misconceptions.” Journal of the American Musicological Society 57 (1): 51–118. 

de Clercq, Trevor. 2019. “The Harmonic-Bass Divorce in Rock.” Music Theory Spectrum 41 (2): 271–284. 

de Clercq, Trevor, and David Temperley. 2011. “A Corpus Analysis of Rock Harmony.” Popular Music 30 (1): 47–70. 

Ferrandino, Matthew. 2022. “Multi-Centric Complexes in Pop-Rock Music.” Intégral 35: 27–43.

Harrison, Daniel. 1997. “Bitonality, Pentatonicism, and Diatonicism in a Work by Milhaud.” Music Theory in Concept and Practice, eds. James M. Baker, David W. Beach, and Jonathan W. Bernard, 393–408. Rochester: University of Rochester Press.

_____. 2016. Pieces of Tradition: An Analysis of Contemporary Tonal Music. New York: Oxford University Press.

Helgert, Lars E. 2008. “Jazz Elements in Selected Concert Works of Leonard Bernstein: Sources, Reception, and Analysis.” Ph.D. diss., Catholic University.

Hook, Julian. 2023. Exploring Musical Spaces. New York: Oxford University Press.

Kaminsky, Peter. 2003. “Composers’ Words, Theorists’ Analyses, Ravel’s Music (Sometimes the Twain Shall Meet).” College Music Symposium 43: 161–177.

_____. 2004. “Ravel’s Late Music and the Problem of ‘Polytonality.’” Music Theory Spectrum 26 (2): 237–264. 

Knapp, Raymond. 2013. “The Sounds of Broadway’s Mean Streets: Setting New York City ‘Edge’ in Show Song.” Studies in Musical Theatre 7 (2): 237–259.

Laird, Paul. 2022. West Side Story, Gypsy, and the Art of Broadway Orchestration. New York: Routledge.

Lewin, David. 1987. Generalized Musical Intervals and Transformations. New Haven: Yale University Press. 

Martins, José Oliveira. 2015. “Bartok’s Polymodality: The Dasian and Other Affinity Spaces.” Journal of Music Theory 59 (2): 273–320. 

_____. 2019. “Scalar Dissonance and the Analysis of Polytonal/Modal Mismatch in Twentieth-Century Music.” Musurgia 2019 (3): 49–87. 

Mellers, Wilfrid. 1964. Music in a New Found Land: Themes and Developments in the History of American Music. New Jersey: Transaction Publishers.

_____. 2001. “The Narrative and Thematic Significance of Music in West Side Story.” In Readings on West Side Story, ed. Mary E. Williams, 67–76. San Diego: Greenhaven Press.

Mugmon, Matthew. 2019. Aaron Copland and the American Legacy of Gustav Mahler. Rochester: University of Rochester Press. 

Muniz, John. 2019. “A Tendency-Transformational Model of Enharmonic Modulations and Related Phenomena.” Music Theory Spectrum 41 (1): 1–20.

Myler, Derek. J. 2021. “Lewin’s Dubbit, Husserl’s Post-horn: A Multistable Model of Polytonal Perception.” Presented at the Society for Music Theory Annual Meeting (virtual). 

Nagel, Julie J. 2010a. “Psychoanalytic and Musical Ambiguity: The tritone in ‘Gee, Officer Krupke.’” Journal of the American Psychoanalytic Association 58 (1): 9–25. 

_____. 2010b. “Melodies in My Mind: The Polyphony of Mental Life.” Journal of the American Psychoanalytic Association 58 (4): 649–662.

Nobile, Drew. 2015. “Counterpoint in Rock Music: Unpacking the Melodic-Harmonic Divorce.” Music Theory Spectrum 37 (2): 189–203. 

_____. 2020. “Double-Tonic Complexes in Rock Music.” Music Theory Spectrum 42 (2): 207–226. 

_____. 2023. “Sondheim’s Dissonant Tonality,” in Here for the Hearing: Analyzing the Music in Musical Theater, eds. Michael Buchler and Gregory Decker, 35–62. Ann Arbor: University of Michigan Press. 

Pomeroy, Boyd. 2004. “Tales of Two Tonics: Directional Tonality in Debussy’s Orchestral Music.” Music Theory Spectrum 26 (1): 87–118. 

Posen, Thomas W. 2016. “Modeling Compositional Grammars in Leonard Bernstein’s West Side Story (1957).” MM Thesis, University of New Mexico.

Reese, Alan. 2020. “Examining Keyboard Bitonality in the Middle-Period Music of Karol Szymanowski.” Music Theory Spectrum 42 (2): 305–325.

Rings, Steven. 2011. Tonality and Transformation. New York: Oxford University Press.

Simeone, Nigel, ed. 2013. The Leonard Bernstein Letters. New Haven: Yale University Press.

Smith, Helen. 2016. There’s a Place For Us: The Musical Theatre Works of Leonard Bernstein. New York: Taylor and Francis. 

Straus, Joseph N. 2014. Harmony and Voice Leading in the Music of Stravinsky. Music Theory Spectrum 36 (1): 1–33.

Swain, Joseph P. 1990. The Broadway Musical: A Critical and Musical Survey. New York: Oxford University Press.

Temperley, David. 2007. “The Melodic-Harmonic ‘Divorce’ in Rock.” Popular Music 26 (2): 323–342. 

Tymoczko, Dmitri. 2002. “Stravinsky and the Octatonic: A Reconsideration.” Music Theory Spectrum 24 (1): 68–102.

van den Toorn, Pieter. 1983. The Music of Igor Stravinsky. New Haven: Yale University Press.

Wells, Elizabeth A. 2010. West Side Story: Cultural Perspectives on an American Musical. Lanham, Maryland: Scarecrow Press.

1. Thomas Posen (2016) supplies a transformational analysis in a more tonally neutral realm, emphasizing set theory. Joseph P. Swain (1990) and Elizabeth Wells (2010) discuss several passages from a theoretical bent, and Lars Helgert (2008) provides close analytical readings of jazz elements in Bernstein’s concert works. Helen Smith’s study (2016) focuses on several dimensions:  the intersection of tritones and fifths, rhythm and meter, motivic development, and counterpoint.
2. Joseph Straus’ 2014 article exhaustively shows how a pair of perfect fifths has great explanatory power in Stravinsky’s harmony and voice leading. Steven Baur (1999, 564) traces Stravinsky’s exposure to the C/F$$\sharp$$ triadic superimposition to a performance of Jeux d’eau (composed in 1901), and only after hearing it, did the chord appear in Rimsky-Korsakov’s hand (ibid., 567). Significantly, Milhaud viewed that the clashing of even the most distant relationships—even the superimposition of these two particular triads—can be considered polytonal rather than atonal (see Amos 2007, 48).
3. Bernstein believed that Schoenberg’s twelve-tone music presents ambiguities “too huge to be grasped,” whereas Berg’s “positive ambiguities” stem from his explicit applications of tonality within his tone rows (ibid., 297).
4. One such recent examination of simultaneous bitonality is found in Reese (2020) on the music of Karol Szymanowski, whose “keyboard” polytonality is often generated by the superimposition of black and white keys. Holly Bergeron-Dumaine (2018) investigates the interaction of concurrent strata, delineating “syntactic” (pitch and duration) versus “statistical” (orchestration and timbre, tempo, and gesture) differentiation (40).
5. The central focus of Bernstein’s analysis tracing the origin of Wagner’s motives to Berlioz’s Romeo and Juliet (ibid., 227), and not as much on the Prelude’s tonality. He does note, however, that the most frequently occurring pitches in the first two phrases of the Prelude form a G$$\sharp$$ diminished 7^th, implying four possible keys A, C, E$$\flat$$, and F$$\sharp$$.
6. See Bailey (1985, 122), who first established the “double-tonic complex.” Scholarship investigating multiple tonics is found in Pomeroy (2004) on Debussy and BaileyShea (2007) on Wolf; more recent work on multiple centers in popular music appears in Nobile (2020), specifically on the double-tonic complex, and Ferrandino (2022), who extends the theory to “multi-centric” complexes. I do not employ their specific terms, instead opting for successive versus simultaneous bitonality, which embraces the distinction between horizontal and vertical manifestations of bitonality.
7. This example is reproduced from Helgert (218). In his analytical chapters, he illustrates the usage of blues scale degrees in Bernstein’s Sonata for the Piano, II(203–04); Clarinet Sonata (213–217); Symphony no. 2, “The Seven Stages” (234–237) and “The Masque” (247); and Touches: Chorale, Eight Variations and Coda (297, 302–303), especially within the application of the octatonic collection (310).
8. Most recently, Laird (2021) has uncovered, through studies of Bernstein’s sketches, the processes of West Side Story’s orchestration.
9. Thomas Posen, in his 2016 master’s thesis, identifies the opening (016) set class as source material, tracing this opening set through more tonally agnostic transformations.
10. For example, she cleverly illustrates that the minor second between the trichord’s semitone transforms into a whole step in “Somewhere” and “Procession” (ibid., 152).
11. As Smith notes, the tritone is only absent from “America,” “Somewhere,” and “I Feel Pretty” (2016, 152).
12. Though it was the opinion of prominent scholars that the concept of polytonality was “dubious” (Berger 1963, 22–23) or, even worse, a “horror of the musical imagination” (van den Toorn 1987, 63–64), these cries are heavily exaggerated. As Daniel Harrison has suggested, the ridicule for the compositional practice of polytonality uncharitably extends to those analysts who wish to uncover the procedure (1997, 394). In support of this analytical perspective in Stravinsky, Dmitri Tymoczko proclaims that the “music itself will necessarily be our last court of appeal” (2002, 85). Fortunately, since Bernstein has endorsed the compositional procedure with such affirmation, perhaps an analyst can be at peace uncovering “the effects and results of this procedure, as well as the conditions under which it flourishes” (Harrison 1997, 394).
13. Kaminsky terms this semitonal class as a “T11 superimposition”; see 258–261.
14. In Ex. 15, de Clercq discusses—at the end of Joni Mitchell’s “Blue”—widespread instances of left-handed “power chords” conflicting with triads performed in the right hand, ending with an instance of an A-E “power chord” as superposed below an E-major triad above it (2019, 283–84).
15. Ferrandino’s “multi-centric complexes” provide an alternative take on Nobile’s and de Clercq’s “divorce paradigms” (2022, 32).
16. Martins summarizes the polytonality “debate” as revolving around two theoretical tensions: 1) polytonality as a product of the compositional craft versus one’s perception of a layered structure; 2) each layer has explicitly activated functional keys versus (only) preserving a tonal character (2019, 50). – In separate work, he discusses models for polymodality—also involving scale segment interaction—in Bartok (see Martins 2015).
17. Another excellent analysis using Rings-style analysis is found in Julian Hook’s recent Exploring Musical Spaces, tracing the scale degree functions through harmonic settings of the G-C$$\sharp$$ tritone in Debussy’s Prélude à l’après- midi d’un faune. See, in particular, 265–267.
18. This interpretation of $$\flat\hat{7}$$ supports Bernstein’s stance on the overtone series as a backbone for universal tonality in his first Harvard lecture, “Musical Phonology.” More recently, Harrison has discussed overtone-series hierarchies as “overtonality” (2016, 17); Harrison also explores “colored triads” (107–109) and “polychords” (109–111).
19. The D$$\sharp$$ as $$\flat\hat{5}$$—reflecting Bernstein’s early writings on the blues scale, and consistent with the other “lowered” scale degrees (Example 4)—could be interpreted as $$\sharp\hat{4}$$ in A major, consistent with its spelling. Beyond blues, Bernstein was also likely inspired by the first demonstration in his first Harvard lecture—the opening of the “fierce and prophetic” Copland Piano Variations (1976, 4), which prophecies the “Prologue”’s A M/m triad in m. 3.
20. With the processual toggling between C and A tonics, Derek Myler (2021) might analyze such a passage under the umbrella of a “multistable” model.
21. Bass features similar examples of $$\flat\hat{6}$$ substituting for $$\hat{5}$$ in Kabalevsky’s Op. 60, no. 2, m. 3 (ibid., 200-201) and Prokofiev’s Piano Sonata no. 8, Op. 84 (ibid. 208). The transformation of G$$\sharp$$, a leading tone tending upward, to A$$\flat$$, tending downward, would be described by John Muniz (2019) as a “tendency transformation.”
22. Nobile (2023) discusses a very different strategy from Bernstein’s lyricist for West Side Story, Stephen Sondheim, whose bass lines are “firmly grounded in standard tonal practice, generally centering on $$\hat{1}$$, $$\hat{4}$$, and $$\hat{5}$$ with various levels of embellishment. In fact, the simplicity of the bass is what allows him to incorporate so much dissonance.” In stark contrast with Sondheim, Bernstein often destabilizes the harmonic underpinning, such that the melodic material resists a concrete tonal interpretation.
23. Wilfrid Mellers describes it as follows: “The persistent dislocation of the accents is both physical and emotional, and the tendency to bitonality—or rather to two-part writing in which one part is unresolved appoggiatura to the other—suggests their disconnectedness.” (1964, 429)
24. A similar style of analysis was performed by de Clercq and Temperley of the Beatles’ “Hey Jude” (2011, 57).
25. Posen (2016) analyzes the schematic frames of the different character groups interacting on stage and toward the audience (ibid., 79–80), and supplies a semiotic and contrapuntal interpretation of the original “Tonight” tune as sung by Tony in canon with violins (83–87).
26. Hook would describe this as a “signature transformation” (2023, 550–568).
27. Posen argues that the “Rumble” “does not follow tonal syntax, even though [Bernstein] used what he considered ‘pure tonal’ compositional building blocks” (2016, 44).