Reimagining Fauré’s Harmony

Gilad Rabinovitch

Abstract

This article explores the nexus of analysis and recomposition in engaging Fauré’s harmonic ambiguity. I argue that Fauré’s harmony can be partially explained through the traditional model of the Rule of the Octave (RO), vestiges of which were still present in the partimento training of nineteenth-century French musicians (Cafiero 2007; Gjerdingen 2020, 2021). I claim that Fauré manipulates segments of the traditional RO in idiosyncratic ways, which partially explains his ambiguous harmonies (cf. Lewin 1986; Smith 1986; Agawu 1994; Hyer 1996; Smith 1997). Along with musical analyses, I employ recomposition (Holtmeier 2002; BaileyShea 2007; O’Hara 2017), which helps to articulate aspects of Fauré’s harmonic usage. Recomposition is thus no longer just a conventional foil against which the original is pitted; rather, it is an opportunity to test our evolving understanding of Fauré’s idiom (Tait 1989; Greer 1991; Phillips 1993; Johansen 1999; Sobaskie 1999; Caron 2002; Pau 2016; Rings 2021).

View PDF
Return to Volume 36

Keywords and phrases: Gabriel Fauré; Rule of the Octave; harmonic ambiguity; recomposition; model composition.

“We understand and appreciate a work not only in terms of the possibilities and probabilities actually realized, but in terms of our sense of what might have occurred in a specific compositional context: that is, in terms of the work’s implied structure.” (Meyer 1989, 32)

1. Recomposition Vignette: Comparing Two Types of Recomposition

Example 1a presents an unusual sequence taken from Gabriel Fauré’s Nocturne No. 5 for piano in B$$\flat$$ major, op. 37. This passage does not appear after a literal double bar, but the preceding materials are an exact repetition of a phrase that is notated twice. Therefore, this passage sounds as if it comes immediately after a first double bar within binary form. This is the prototypical position for Joseph Riepel’s and Robert Gjerdingen’s Fonte, Monte, and Ponte (Gjerdingen 2007). In this case, a highly unusual descending Fonte sequence is used. The recomposition in Example 1b shows a path not taken, with which Fauré’s music is in dialogue—a simple sequence moving from tonicized ii to the home key.¹ Projecting Fauré’s music into a simpler framework helps us appreciate his manipulation of norms still relevant to listening to this passage. In the actual piece (Example 1a), the melody initially suggests a transposition down by a half step, yet the harmonic sequence descends by a major third. While it is difficult to discern chordal qualities with so much inner-voice contrapuntal motion, both m. 19 and m. 24 seem to outline a half-diminished seventh chordal quality: A$$\flat$$–C–D–F and B$$\flat$$–D$$\flat$$–F$$\flat$$–A$$\flat$$. In nineteenth-century usage, a half-diminished seventh chord likely usually functions as ii⁷ or vii⁷ respective to a local tonic: in Fauré’s functional progressions, this sonority is typically used as vii⁷/V, ii⁷, or vii⁷ (Tait 1989, 28–29). 

By outlining a similar chordal quality, Fauré creates a harmonic parallelism that is undermined by the asymmetrical bass segments: A$$\flat$$–G–C in the first part of the Fonte is answered by B$$\flat$$–E$$\flat$$–A$$\flat$$ in its second part. If we want to understand Fauré’s dialogue with preceding musical norms, the juxtaposition of Examples 1a and 1b is useful. But if our goal is to understand the particularities of Fauré’s idiolect, Example 1b leads us astray: it is unlikely that Fauré would have written such a bland passage that does not have even a single subverted harmonic implication. Though Example 1b is analytically useful, it does not contribute directly to describing Fauré’s idiom. The rest of the recompositions in this article are style-bound: I attempt to reimagine musical phrases that represent paths not taken in Fauré’s harmonic language. Of course, I do not claim that my reimaginings are just as Fauré would have recomposed them; I simply believe that this is a productive way to engage Fauré’s harmony and our evolving understanding of it.

Let us now turn to a reimagined version of a brief passage by Fauré, which, unlike Example 1b, does aim to emulate the composer’s idiolect. Example 2a presents a passage from the “Libera me” of Fauré’s Requiem, op. 48, which ends on a Fauré-style ii$$^{6}_{5}$$­–I plagal cadence in A minor (with a Picardy third).² In contrast, recomposed Example 2b cadences in F major. Example 2b exploits Fauré’s tendency to be discussed below to use $$^{5}_{3}$$ and $$^{6}_{3}$$ sonorities on a bass note (often $$\hat{5}$$) interchangeably: the A-minor sonority in m. 15 is thus reinterpreted as “III⁶” of F major. Of course, the unusual sixth above the bass resolves contrapuntally and leads to a tonally clearer V⁷ sonority. The contrast between the style-bound recomposition of Example 2b and the generic Example 1b is clear: while Example 2b attempts to emulate Fauré’s style, Example 1b makes an analytical point by alluding to broader common-practice norms.

I will argue below that the Rule of the Octave (henceforth: RO), a traditional model for bass scale harmonization, explains parts of Fauré’s harmonic usage, though with important modifications and play upon it.³ Fauré veils this template, among other ways, by conflating $$^{6}_{3}$$ and $$^{5}_{3}$$ sonorities with one another in positions across the bass scale where the other sonority is expected. This is part of Fauré’s broader tendency to take traditional bass patterns and play upon them through unusual upper voices. For now, let us observe that in Example 2a, mm. 13–16 are plausibly the scale segment $$\hat{1}$$–$$\hat{2}$$–$$\hat{3}$$–$$\hat{4}$$ in A minor, with $$\hat{1}$$ carrying an unusual $$^{6}_{3}$$ sonority and $$\hat{4}$$ carrying a typical ø$$^{6}_{5}$$ sonority; in the recomposed Example 2b, mm. 11–16 are plausibly $$\hat{2}$$–$$\hat{3}$$–$$\sharp\hat{4}$$–$$\hat{5}$$ in F major, with $$\hat{5}$$ initially carrying a disorienting $$^{6}_{3}$$ sonority. This foretaste of my analysis and argumentation suggests that I will be attuned to bass patterns, upper-voice structures, and the tonal implications of the RO.

Several background discussions are necessary in order to tie together the strands of this article. The next section situates my position on analytical recomposition within the literature on this technique. I then move on to engage sources on harmonic ambiguity in general and the Anglo-American music-analytical literature on Fauré’s harmony in particular. In the following sections, I demonstrate at length how Fauré’s ambiguity can be conceptualized (and alternative paths recomposed) through adaptations to the traditional RO. This is not only a practical model for harmonizing bass scale segments, but also a historical tool for conceptualizing tonal shifts (Byros 2009, 2012; cf. Lester 1992). Though Fauré’s early training at the École Niedermeyer is somewhat shrouded in mystery—it is unclear if practical partimenti methods adopted at the Paris Conservatory (including the RO) were also in use at the École—I show that the RO (with significant modifications) explains some aspects of the composer’s harmonic usage. I incorporate several short examples and two vignettes, which focus on the Fantasy for Flute and Piano and the “Introit & Kyrie” from the Requiem, demonstrating how the RO and its creative potentials can elucidate aspects of Fauré’s harmony; recomposition is thus no longer a straw man against which the musical text is set in relief, but rather an opportunity to test our evolving understanding. I revisit Richard Cohn’s analysis of the “Introit & Kyrie,” which offers a chromatic explanation of a challenging passage through the nexus of an augmented triad; as I demonstrate, the RO and its manipulations offer a diatonic lens that complements Cohn’s perspective. Finally, I offer Debussy-Fauré mashup fragments based on Claude Debussy’s “Clair de lune” from the Suite bergamasque and reflect on potential echoes of Fauré in one of Erik Satie’s Gymnopédies. Thus, I demonstrate how well-known pieces can be reheard or reimagined through the sieve of Fauré’s harmony. My general goal is to engage certain aspects of the composer’s harmony through analysis and recomposition, yet I should emphasize that I am not in a position to provide a formal statistical account of his harmonic usage; I have relied here on my intuitions formed through several years of studying the composer’s style and works, but the RO is certainly only one template among many that he used.

2. Recomposing Fauré

In the opening vignette above, I presented two types of recomposition: the first type is attuned to underlying musical norms with which Fauré is in dialogue, but not to the composer’s harmonic idiolect, while the second is style-bound, actively attempting to emulate the composer’s harmonic usage. The remaining recompositions in this article follow the latter approach: I am interested in finding synergies between music analysis, recomposition, and model composition in order to achieve greater clarity regarding Fauré’s harmonic usage. In this way, theoretical descriptions of Fauré’s harmonic style can be tested “hands-on” via a brief recomposition; the process of recomposing may potentially lead to new explanations or, at the very least, to articulating some of the intuitions involved in creating music in a historical style, even if they are not ready yet to be systematized. Indeed, certain aspects of my recompositions, such as the usage of pedal points, were done intuitively without theorizing, but with the goal of emulating the composter’s style. Other aspects—related to the RO—are more clearly theorized at this stage of my ongoing research on the composer.

William O’Hara (2017, 56) proposes five general types of recomposition (Table 1): corrective recomposition, which proposes a “correction” to the actual score which the analyst finds flawed; model recomposition (not to be confused with my style-bound recomposition), which is when the analyst changes the musical surface in order to bring it closer to a presumed underlying model; theory building, which is when the recomposition serves as “evidence” for an explanatory system; analytical recomposition, or when recomposition itself serves as an analysis of music through music; and perceptual/cognitive/phenomenological recomposition, which is when the recomposition serves an argument about how the piece is perceived, processed, or experienced.

Corrective	Proposing a more “correct” way that a piece of music should have gone
Model recomposition	Recomposing a piece to bring it into closer alignment with an underlying model
Theory-building	Recomposing a piece in order to use it as theoretical “evidence”
Analytical	Recomposition as a form of non-verbal analysis
Perceptual/cognitive/phenomenological	Recomposition as an argument about how a piece of music is perceived, processed, or otherwise experienced

Example 1b belongs to O’Hara’s category of “model recomposition” in the sense that it fits the composer’s unusual passage into a mold with which Fauré is in dialogue. Most of my recompositions can also be said to have a cognitive (or at least experiential) motivation: they set into relief harmonic implications not realized. Since I propose that the RO might be an explanatory model for aspects of Fauré’s harmony, one might say that my recompositions also serve theory building. In all these ways, my recompositions follow well-trodden paths and blend some of O’Hara’s categories. Yet I would like to argue that a synergy of analysis, recomposition, and model composition can—and should—become a testing ground for our evolving understanding of an idiom, Fauré’s or otherwise. If our analytical tools are effective descriptors of musical styles, they ought to help us compose in them; conversely, composing in historical styles may articulate aspects of musical usage that might otherwise go unnoticed.⁴ This synergy is not commonly applied in music theory and analysis: analyses are generally presented as descriptive or explanatory statements without an attempt to reverse-engineer them as creative tools.

Another important influence on this inquiry is Ludwig Holtmeier’s (2002) article “Reconstructing Mozart.” Holtmeier describes an analytical and recompositional tradition practiced in German conservatories in which a passage is creatively manipulated to make sense of it, articulating musical and analytical intuitions. I am also inspired by Marc Hannaford’s (2019, 2020) engagement of free improvisation, which draws on his practical experience as an improvising musician: by stopping a recorded improvisation and continuing with an improvised gesture of his own, he speculates on unrealized potentials. He writes that his responses help to gain “a more robust understanding of the actual [improvised] response by considering its similarities and differences to other, hypothetical responses” (2019, 82). Further, he notes that “both Cook [1987] and BaileyShea emphasize that recomposition is a process of weighing alternatives—in ecological terms these theorists describe recomposition as an exploration of musical materials’ multiple affordances” (2019, 83). Hannaford works in free improvisation where harmonic constraints are looser, yet his notion of finding ecologically valid responses is useful here. If my recomposition attempts are on the right track, then they reflect some harmonic constraints of Fauré’s style.

There are additional relevant precedents for my project. Vasili Byros (2015) composes a prelude in the style of Johann Sebastian Bach, demonstrating how historical pedagogies and present-day model composition help reconstruct stages of the creative process. Matthew BaileyShea (2007) creates a hybrid version of several settings of a poem by Goethe: his mashup reveals intertextual links among the settings, contributing to our explicit understanding of the connections between them. My concluding Fauré–Debussy mashup fragments are inspired by BaileyShea, passing an early Debussy piece through the sieve of Fauré’s harmony. Of course, Peter Schubert’s important work on the Renaissance style (e.g., 2008, 2011, 2020) engages historical notations and treatises both analytically and creatively through model composition and improvisation.⁵

3. Fauré’s Harmonic Ambiguity

Fauré’s enigmatic harmonic language has already been treated in some insightful music-analytical studies, which are generally focused on analysis rather than composition or recomposition. Taylor Greer (1991), Edward Phillips (1993), and James Sobaskie (1999) employ Schenkerian theory to analyze Fauré’s technique. Sobaskie (1999) claims that the principle of allusion is central to the composer’s works: this manifests itself, inter alia, through allusions to modality and through veiled references to keys other than the tonic. In contrast to these Schenkerian analyses, my inquiry resonates more strongly with studies that explore the composer’s work closer to the surface, where I believe its harmonic charm lies. Thus, Ken Johansen (1999) discusses Fauré’s harmonic ambiguity and the multiple tonal implications of chords from a functional-chordal perspective; Sylvain Caron (2002) describes the composer’s harmonic usage in service of model composition (Écriture in French-language curricula). Though Caron frames his inquiry as background for model composition, he discusses the latter activity only in general terms (2002, 48–49, 73–75) without providing passages composed by his students or himself that might show how his analyses serve that goal. I will return below to Caron’s analysis of Nocturne No. 6, in which he shows how the musical surface is a complex reaction to a conventional bass formula. Andrew Pau (2016) discusses plagal systems in the songs of Fauré and Henri Duparc: given the influence of Hugo Riemann’s dualist harmonic theories in France—mediated by Vincent d’Indy, a friend of both Fauré’s and Duparc’s—Pau provides an analytical exploration of songs by the two composers. Among other techniques, Pau shows tonic expansions involving plagal sonorities as well as deeper structural manifestations of a dualist T–D–S–T model. Pau notes the paucity of French-language examples in Daniel Harrison’s (1994) revival of harmonic dualism and argues that the songs of Fauré and Duparc are a fertile ground for this approach. In analyzing Fauré’s Nocturne No. 4 below, I will borrow some dualist notions to explain the function of an elusive chord. I should stress, however, that my usage of the term “plagal cadence” refers to $$\hat{4}$$–$$\hat{1}$$ bass motion, often harmonized according to the RO, rather than to particular details of the dualist apparatus, say, T–D–S–T functional cycles or Harrison’s decomposition of chords into functional scale degrees.

In discussing Examples 2a and 2b above, I have observed that Fauré tends to use $$^{5}_{3}$$ and $$^{6}_{3}$$ sonorities interchangeably, at times where the other sonority would have been expected. In applying these ideas to Fauré, I am indebted to Peter Smith’s analyses of music by Johannes Brahms and others. Smith (1997) discusses ambiguous $$^{6}_{3}$$ chords in Brahms, whether they are derived from $$^{5–6}$$ contrapuntal motion, serve a harmonic function, or can be understood through both lenses. My reasoning also echoes Smith’s discussion of the second movement of Franz Schubert’s Sonata in A Major, D. 664 (not shown), in which the opening D–F$$\sharp$$–B sonority is not only a $$^{6}_{3}$$ contrapuntal displacement of the opening $$^{5}_{3}$$ tonic (or $$^{6}_{3}$$–$$^{5}_{3}$$), but also sows the seeds for future emphasis on B (Smith 2000, 6–13). Regarding the opening of Brahms’s Intermezzo in E Minor, op. 119, no. 2 (not shown), Steven Rings writes that “the Roman numeral hearing also has an off-balance quality, in which the C six-three chord is a displacement of an E-minor five-three” (2011, 131). Without getting into the thicket of Rings’s multi-faceted approach, I would like to point out that from the present angle, Brahms’s piece opens with a recognizable $$\hat{1}$$–$$\hat{4}$$–$$\hat{5}$$–$$\hat{1}$$ bass schema, which remains noticeable despite the unusual $$^{6}_{3}$$ above $$\hat{1}$$.⁶ Though I do not share the theoretical apparatuses of Smith or Rings, my discussions of ambiguities associated with $$^{5}_{3}$$ and $$^{6}_{3}$$ sonorities are indebted to theirs. I refer below to $$^{6}_{3}$$ where $$^{5}_{3}$$ is expected as a “$$^{6}_{3}$$ substitution” even if it is resolved contrapuntally, due to the striking tonal effect of this sonority, of which Fauré is so fond: I believe that the disorienting tonal impression created by a $$^{6}_{3}$$ where a $$^{5}_{3}$$ is expected is crucial to the composer’s harmonic usage.

My article is also in dialogue with additional inquiries on harmonic ambiguity (Smith 1986; Lewin 1986; Agawu 1994; Hyer 1996). Let us look at a quotation from Lewin, who writes: “According to Husserl’s theory, what I am perceiving—let us call it Perception(a)—is a hugely complex network of things, things including other perceptions, their relations among themselves, and their relations to Perception(a) itself” (1986, 332). Lewin’s perceptions at individual timepoints are not only hyper-local phenomena but are also related to tonal schemata like the PAC or “Deceptive Cadence” progressions (see his examples in 1986, 331). Lewin suggests to “mistrust anything that tells you not to explore an aural impression you have once formed,” (359–360). Rephrasing this dictum from the present angle, one might say: “mistrust anything that tells you not to reimagine the music as it could have been” as part of the back-and-forth of analysis and practice.

Kofi Agawu (1994) is more skeptical of harmonic ambiguity than Lewin. He argues that passages generally cease to be ambiguous once a context is taken into account (86). Moreover, he argues that ambiguous tonal passages generally follow an “irreversible ambiguity-to-clarity order” (91): this is a valid generalization for much common-practice music, but it does not apply so strongly to Fauré. The fact that Agawu thinks it inappropriate to interpret the first chord of Beethoven’s Symphony No. 1 as a German chord but discusses the V⁷ vs. Ger+6 ambiguity in a song from Robert Schumann’s Dichterliebe (89–92) implies that he interprets harmonic ambiguity based on composers’ individual usage, not only on broad common-practice norms. Agawu writes:

The “I do not know” type of ambiguity is a weak kind, one that need not detain us here so long as ours is a theory-based context. Ambiguity in the stronger sense is a product of both prospective and retrospective views. After several hearings, I know (of course) what happens to the opening chord, but I might still choose to model a hearing in which the dual meaning of the opening chord plays an important part. I might argue that the richness of the experience derives not from not knowing what the resolution of the opening chord is going to be but from self-consciously enacting a state of harmonic ignorance, from temporarily unknowing what I already know. (1994, 93)

Fauré’s elusive harmony represents a strong kind of ambiguity, one in which (especially) prospective implications are constantly thwarted. As Rings writes, after the works of philosopher-musicologist Vladimir Jankélévitch, “this music becomes more elusive, not less, the closer we listen” (2021, 236). Thus, in Example 3a at the first asterisk, an augmented triad fails to provide us a clear i or V chord in B minor; at the second asterisk, a French augmented sixth chord implies either E minor or B minor (but does not really resolve the ambiguity); the cadence that appears to be in E minor (at the third asterisk) does not give us a clear tonic or dominant in that key (Rings 2021, 244).⁷ This passage is an apt demonstration for the ways in which Fauré’s ambiguities linger on rather than progressing in Agawu’s “ambiguity-to-clarity” order.

My recomposition in Example 3b completes one of the tonal schemata that Rings invokes by embedding the French augmented sixth chord within a more predictable context despite the unusual subsequent modal coloring and missing leading tone. In other words, I realize a prospective implication in a more schematic manner in comparison to Fauré’s passage. Despite the neo-Renaissance style of this passage, the local tonal schema “augmented-sixth resolution” is still relevant to our experience of it.⁸

In a discussion of harmonic ambiguity and “second immediacies” in the opening of Beethoven’s Eroica, Brian Hyer (1996, 81) finds the hearing of a shift to G minor—as suggested in a review by one of Beethoven’s contemporaries—to be unpersuasive. Byros (2012) takes an alternative approach by surveying reactions to and analyses of Beethoven’s opening passage, including the review discussed by Hyer: his survey suggests that, over time, analysts and critics have tended to hear mm. 7–10 more monotonally in E$$\flat$$ major rather than G minor. Byros claims that the “le-sol-fi-sol” schema suggested to historical listeners the G-minor hearing, whereas the more monotonal E$$\flat$$-major hearing of this passage relates to the “common-tone diminished seventh” schema, which was in vogue later in the nineteenth century. In other words, Byros believes that the more monotonal hearings are anachronistic, based on the enculturation of listeners who had less exposure to the “le-sol-fi-sol” schema and more exposure to the “common-tone diminished seventh” schema. Byros’s elegant reasoning reminds us that the perception of tonality relies on the recognition of conventional tonal schemata: as we shall see later, the RO was also a historical model for conceptualizing tonal shifts in ways that seem highly localized to us given our present-day monotonal understanding (Byros 2009, 2012). I will not attempt here to track diachronic change in harmonic usage patterns as Byros does: my underlying assumption is that common-practice norms, including those encapsulated in the RO, are still relevant to our experience of Fauré’s music.

In discussing the final cadence of Maurice Ravel’s L’enfant et les sortilèges (Example 4), Damian Blättler (2017, [1]) contrasts the clear functional dominant-tonic resolution of the bass motion with the non-traditional nature of the upper voices.⁹ While Blättler does not use the word “schema,” he asserts, after Gjerdingen (2007, 16–19), that “one of the aims of music theory is to describe how musical structures relate to shared cultural assumptions between audiences and producers” (2017, [43]). Though his upper-voice structures are more traditional than those of Ravel, Fauré tends to use the “wrong” triads or seventh chords above conventional tonal bass schemata. The opening of Nocturne No. 6 (Example 5) will be discussed below at length. At present, let us observe that its first three measures contain a simple tonal bass schema: $$\hat{1}$$–$$\hat{5}$$–$$\hat{6}$$–$$\hat{7}$$–$$\hat{1}$$–$$\hat{4}$$–$$\hat{5}$$–$$\hat{1}$$, which is matched with highly disorienting upper voices. Caron (2002, 59, example 11) proposes a hypothetical harmonization, I–V–IV⁶–V⁶–I–IV–V⁷–I, as a simpler underlying model suggested by the bass. It is as if Fauré’s musical surface is an unusual reharmonization of a simple tonal bass schema. In Example 5, I have highlighted through boxes those chords on $$\hat{5}$$ that Caron annotates as “iii” chords, a point to which I will return below.

The opening of Fauré’s Nocturne No. 7 (Example 6) presents a similar situation: Fauré opens a piece in C$$\sharp$$ minor using a well-worn bass schema, $$\hat{1}$$–$$\hat{4}$$–$$\hat{5}$$. The upper-voice sonorities, however, are far from what one would expect, with both the chords on $$\hat{1}$$ and $$\hat{5}$$ matched with upper-voice $$^{6}_{3}$$ rather than $$^{5}_{3}$$ (or $$^{7 \atop 5}_{3 \atop \phantom{3}}$$) on $$\hat{5}$$. On $$\hat{4}$$, a dom7 chordal quality sounds briefly, invoking B major. As stated earlier, Fauré often substitutes for $$^{5}_{3}$$ with $$^{6}_{3}$$, creating tonal ambiguity, which is present in this passage as well. Of course, the third and fourth dotted-quarter beats in m. 1 may suggest more of a $$^{5}_{3}$$ chord on the tonic, yet the opening, enigmatic $$^{6}_{3}$$ sonority is salient: it only resolves in its own register to G$$\sharp$$₄ on the fifth beat.

The examples considered so far suggest that we must account for multiple factors in analyzing Fauré’s harmony: individual chordal qualities, like those of the half-diminished in Nocturne No. 5 or the French-sixth sonority of Nocturne No. 13, are at times responsible for local tonal orientations. Conventional tonal bass schemata—often reharmonized through unusual upper-voice bass structures—are still relevant as well. The next section focuses on one conventional template: the RO.       

4. Fauré’s Rule of the Octave (RO)

Fauré’s idiosyncratic style has sometimes been linked to his training at the École Niedermeyer. In contrast with the Paris Conservatory, where training methods are well documented (and owe a great deal to the partimento tradition), the curriculum at the École Niedermeyer is less clear to us.¹⁰  Students at the latter institution were exposed to a variety of historical styles, including Renaissance modality. Louis Niedermeyer and Joseph d’Ortigue’s (1859) manual on plainchant accompaniment at the organ has been invoked to explain some of Fauré’s idiosyncratic harmonies.¹¹ Gjerdingen (2021, 60) notes that tastes for and against modality could be found at both the Paris Conservatory and the École Niedermeyer, which makes it difficult to argue that Fauré’s training was the decisive factor in his developing tendencies toward modality. Polemics on the proper harmonization of plainchant, including in modal ways, characterized nineteenth-century French discourse (Christensen 2019): Niedermeyer and d’Ortigue’s treatise is thus part of a broader conversation on tonality, its origins, as well as the appropriate way to harmonize plainchant. Gjerdingen writes:

In the same vein, the harmony book of Gustave Lefèvre has been cited as a special factor influencing the teaching of harmony at the École. Both Lefèvre and Camille Saint-Saëns had ties to Pierre Maleden, whose teacher Gottfried Weber was an important figure in the history of theories of harmony. The problems with connecting Fauré’s unique style to Lefèvre or Maleden are, nevertheless, many. Lefèvre became director of the school only in the year that Fauré graduated (1865), and his book on harmony was still twenty-four years in the future (1889). (2021, 61)

Thus, we cannot assume that Lefèvre’s treatise reflects the very teachings that Fauré would have been exposed to, even if this has become received wisdom in Fauré scholarship (e.g., Chailley 1982). It is well known, however, that the teachings at the École Niedermeyer during Fauré’s studies included a mixture of historical and contemporary styles, including exposure to Renaissance modal music. Perhaps the most interesting feature of Lefèvre’s (1889) treatise is the fact that it demonstrates principles of harmony through a variety of tonal and modal styles.¹²

On the other hand, we do have evidence that Fauré was involved in teaching French-academic harmony as practiced at the Paris Conservatory: some of his harmonization exercises have survived (Gjerdingen 2021). This training tradition reflects the adaptation of eighteenth-century Neapolitan partimenti into the curriculum of the Paris Conservatory in the nineteenth century. Training in this tradition involved complex keyboard harmony and written harmonic-contrapuntal exercises. The fact that Fauré was able to create exercises and realize solutions suggests that he was fluent in it. Moreover, Jean-Michel Nectoux (1991, 6) documents that the training at the École Niedermeyer included “the traditional subjects (solfège, harmony, counterpoint)”—which at least opens the possibility that they were in fact close to the Paris-Conservatory adaptation of Neapolitan partimenti.¹³ Without attempting to solve the mystery of the composer’s early training, I argue that the RO—with some significant modifications—is useful for engaging aspects of Fauré’s harmony.

Gjerdingen (2020) offers compelling analyses of Fauré’s usage of sequence models in conjunction with partimento-based French harmonic teachings. As Giorgio Sanguinetti observes (2012, chapter 9), the partimento tradition has two contrasting modes of associating upper-voice sonorities with a given bass segment: sequentially (moti del basso), with various scale degrees in the bass receiving similar sonorities, or through the RO, with scale degrees receiving different sonorities. In other words, trainees in the partimento tradition or its Parisian adaptation conceptualized bass segments either as portions of sequences or as more directional tonal progressions associated with segments of the RO.¹⁴ There is little doubt in my mind that Fauré’s music has clear echoes of French-academic harmony exercises discussed by Gjerdingen (2020, 2021). For instance, Example 7 (“Libera me” from the Requiem, mm. 18–25) contains a sequence with suspensions that is unmistakably close to this tradition. In engaging a passage like this, we should pay attention not only to an exemplar of a learned historical model—an up-a-fourth, down-a-third bass sequence—but also to its elusive tonal implications.¹⁵ Thus, for instance, m. 24 is a melodic highpoint and also a striking harmonic moment, since it subverts the expected resolution to G minor and starts another chromatic sequential link in a chain with the surprising B$$\natural$$ in the salient bass line. This and many other passages in Fauré’s music call for an eclectic approach, incorporating insights from historical pedagogical models as well as present-day music analysis.

Example 8a shows Alexandre-Étienne Choron and Vincenzo Fiocchi’s (1804) RO, representing a small part of the reception of partimenti in nineteenth-century Paris. Example 8b shows another conventional variant of the RO, which contains $$^{6}_{5}$$ in ascending on $$\hat{6}$$ as well, which is typical in Fauré’s harmonic practice.

Broadly speaking, the RO has several crucial properties that are relevant for conceptualizing some of Fauré’s harmonic progressions:

1. The RO creates associations between particular scale degrees in the bass (respective to a local tonic) and intervals above them, which may be represented as figured bass.
2. As a consequence, the RO associates particular scale degrees with specific chordal qualities in a certain inversion: the identity of the bass scale degree is thus connected to a chord of a certain quality (e.g., \hd, dom7 or “major-minor7”) and a certain figured-bass sonority; these specific associations can orient us tonally in ambiguous passages.
3. The RO creates points of relative stability on $$\hat{1}$$, $$\hat{3}$$ (and to a lesser degree $$\hat{5}$$), as opposed to points of instability on $$\hat{2}$$, $$\hat{4}$$, $$\hat{6}$$, and $$\hat{7}$$, which is something that Fauré retains, though not literally.¹⁶ Fauré tends to match stable scale degrees with triads and unstable ones with seventh chords even if they are “wrong” with respect to the more traditional RO. Of course, $$\hat{5}$$ may also receive its typical dom7 sonority. Whatever the case, the RO associates chordal qualities, inversions, and scale-degree identities in the bass.
4. The RO neatly subdivides into a lower pentachord and upper tetrachord, which is a characteristic that Fauré maintains: he often focuses on either part (sometimes on a truncated upper tetrachord, $$\hat{6}$$–$$\hat{7}$$–$$\hat{1}$$). More generally, the RO lends itself to division into partial bass scale-degree segments with typical upper-voice sonorities.
5. The RO affords opportunities to shift to a different “octave” of a different key (i.e., what one might call a tonicization or a modulation). From the viewpoint of analysis or listening, this affords opportunities to reorient ourselves to a new key in a highly localized context, as opposed to present-day monotonal notions (Byros 2009, 2012; Lester 1992). In style-bound recomposition, the RO helps us reimagine local harmonic implications not realized.

My five bullet points suggest that Fauré uses the RO in somewhat of an abstract fashion, associating bass scale degrees respective to a local tonic with certain types of chords or chordal qualities. Despite this abstraction, however, Fauré maintains central features of the RO. Example 9a tabulates the distinction between stable and unstable scale degrees that the RO creates. Examples 9b and 9c demonstrate how associations between “stable” and “unstable” scale degrees can be maintained even with alternative sonorities, varying the lower pentachord: Example 9b uses a MM7 on $$\hat{4}$$ and a $$^{6}_{3}$$ instead of $$^{5}_{3}$$ on $$\hat{5}$$; Example 9c adds a mm7 on $$\hat{2}$$, softening the progression—or, à la Pau (2016)—making it more plagal. In any case, these fleshed out versions of the abstract Example 9a show how basic properties of the RO can be maintained even when the actual upper-voice sonorities are varied. In other words, even as Fauré matches non-traditional sonorities to RO segments, he often maintains a qualitative distinction between bass scale degrees.

Triad	Seventh Chord	Triad	Seventh Chord	Triad or dom7	Seventh Chord (?) (cf. Example 8b)	Seventh Chord	Triad
$$\hat{1}$$	$$\hat{2}$$	$$\hat{3}$$	$$\hat{4}$$	$$\hat{5}$$	$$\hat{6}$$	$$\hat{7}$$	$$\hat{8}$$
Stable	Unstable	Stable	Unstable	Stable (or dom7 sonority)	Unstable	Unstable	Stable

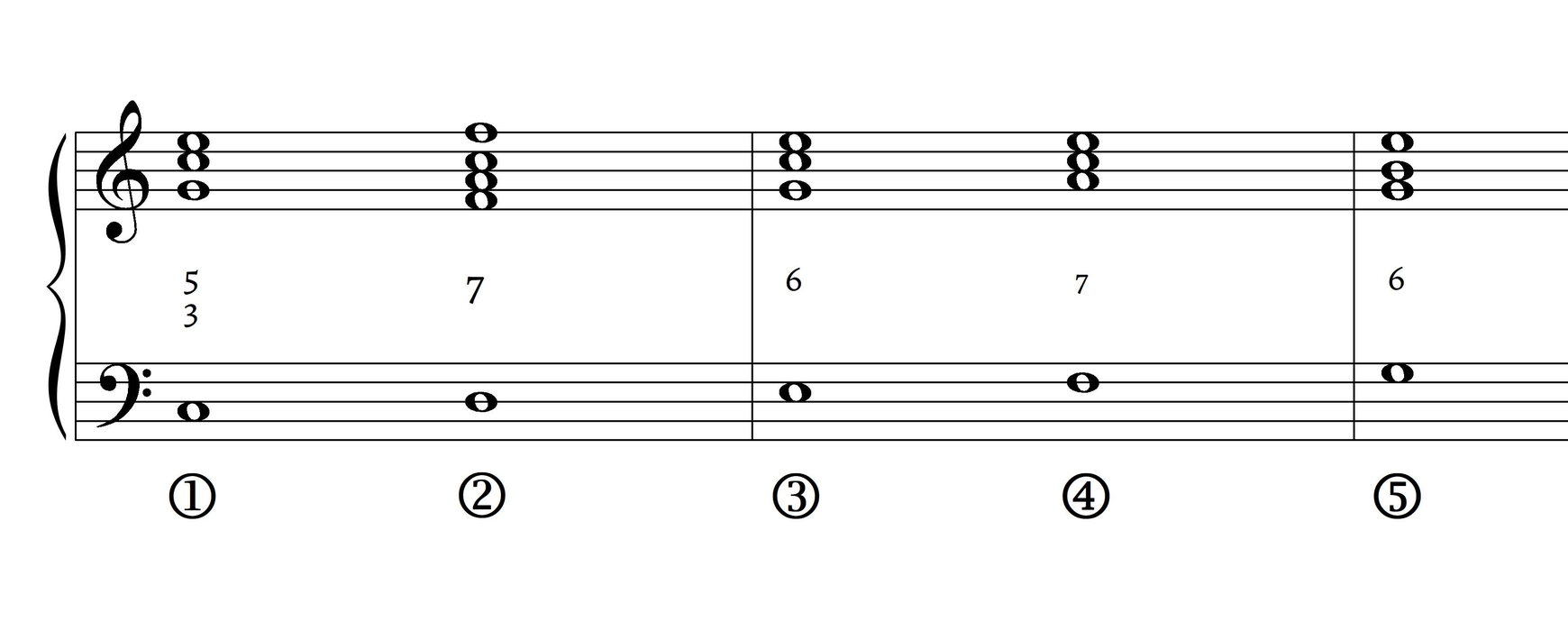
The RO is also a flexible mechanism for conceptualizing tonal shifts, which seem more local to us given our monotonal (and perhaps anachronistic) theoretical lens on tonal music. Historical approaches to tonality, such as those implied in partimenti, were more localized. Lester (1992, 82) discusses an annotated copy of Bach’s D-minor prelude from WTC1, probably stemming from Leipzig in the 1730s or 1740s. Part of this document is reproduced here as Example 10. In m. 14, what is to us a “mere tonicization” of B$$\flat$$ major leads to a shift of bass scale degrees so that a RO-like segment, $$\hat{7}$$–$$\hat{1}$$, is highlighted. A brief tonicization is—according to the view of tonality latent in the RO—a wholesale shift. In this case, a dom$$^{6}_{5}$$ sonority resolving to a root-position sonority indicates a shift to the “octave” of B$$\flat$$ major. Lester writes: “Although it seems narrow-minded to cite such a brief key change [to B$$\flat$$ major], doing so confirms the practicality of the analytic method and early eighteenth-century attitudes towards keys and key changes in general. Both thoroughbass players and composers needed to know the proper chord over each and every bass note. A $$^{6}_{\flat5}$$ chord appears only over the leading tone of a key; hence in measure 14, the bass A is best understood as scale-step 7” (1992, 85). Though Fauré’s usage is non-traditional—and though his style is much later than that of Bach—many passages in his music are still related to the RO, with its rapid conceptual shifts between the “octaves” of difference keys.

From a practical perspective (as in the realization of a partimento), interpreting a bass note as a scale degree respective to some transposition of the RO creates a mental association for the keyboard player with a typical upper-voice sonority; from an analytical perspective, deciphering associations between RO segments, typical sonorities, and local tonal implications can help us to interpret Fauré’s enigmatic harmony. Paying attention to contextual bass scale-degree gambits—as done by Gjerdingen (2007) and Holtmeier (2011)—creates different equivalence classes than those of Roman numerals and inversions. I recognize that my methodology here is not historicist or purist—I attempt to get as much analytical mileage as possible from the entry point of the RO but invoke concepts like inversions and chord functions ad hoc as part of my analytical process.

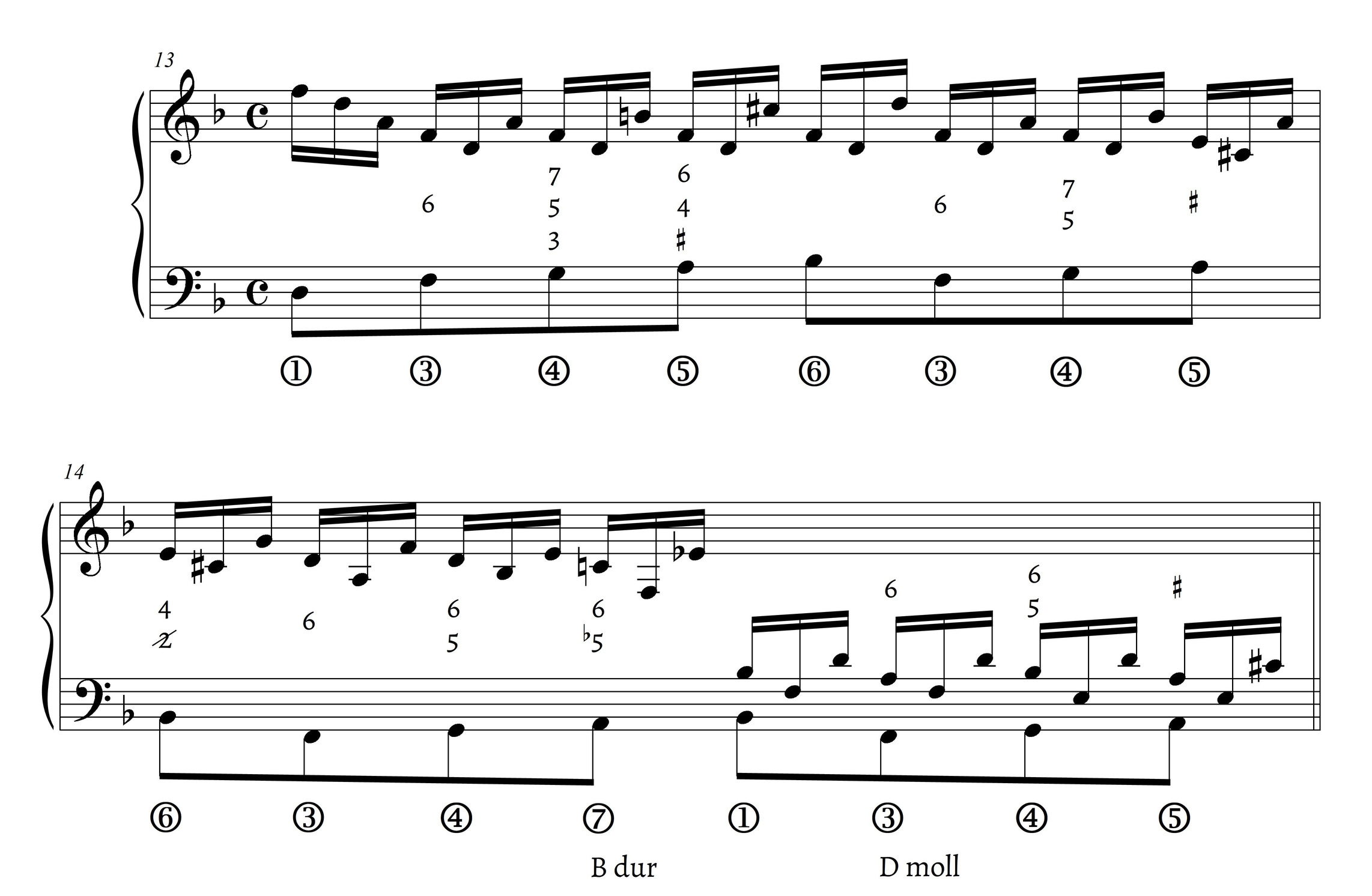
Lester’s example may seem antiquated when dealing with Fauré. An example from a figured bass by Nadia Boulanger (Example 11), Fauré’s student, discussed in Rabinovitch 2020, shows how identifying segments of figured bass as scale degrees in context remained a way to plug in ready-made upper-voice structures. Boulanger’s figured bass was likely written for her American students, who were not trained in the Parisian adaptation of partimenti, hence they needed the scaffolding of figured bass; those trained in this tradition (like Boulanger herself) would have formed mental associations between an unfigured version of these scale segments and upper-voice structures, which could have been used in an unfigured written exercise with a given bass. Of course, my (not so elegant) realization in Example 11 is that of an outsider to the tradition—it was just meant to demonstrate certain aspects of this pedagogical bass.

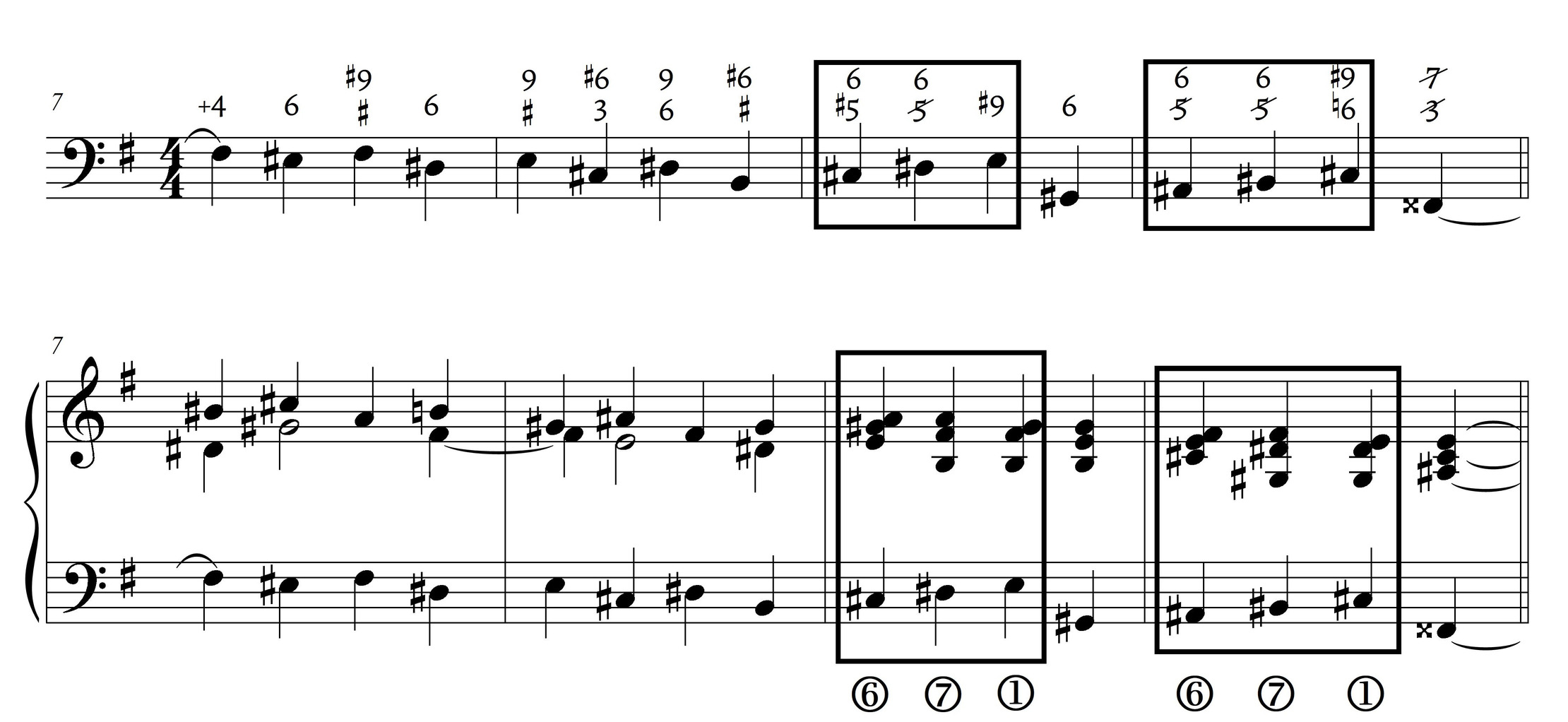
It has become received wisdom in Fauré scholarship that fleeting tonicizations—as conceptualized in Lefèvre’s (1889) treatise—can explain the composer’s idiosyncrasies (Chailley 1982; Nectoux 1991, 227–229; Sobaskie 1999, 183). Yet if we consider the implicit conceptual framework of the RO, a tonicization is a complete shift to a RO starting on a different pitch. 

I have observed above that Fauré tends to place a $$^{6}_{3}$$ rather than a $$^{5}_{3}$$ on $$\hat{5}$$. Other authors have made similar analytical observations, though couched in different terms. Caron (2002, 59–60) discusses the substitution of a “V” chord by a “iii” chord (see Example 5 above). In his analysis of the “Introit & Kyrie” from Fauré’s Requiem—to be engaged in detail below—Cohn suggests that, within a D-minor context, an F-major $$^{6}_{3}$$ chord (i.e., a natural-minor derived “III⁶”) functions as dominant (2012, 54–55). Though these theorists do not allude to the RO, my intuitions about Fauré’s usage coincide with theirs: they suggest the possibility that a “V” chord be substituted by a “III[⁶]” chord. I believe that Fauré’s harmonic usage conflates $$^{5}_{3}$$ and $$^{6}_{3}$$ sonorities more broadly: we have seen in Example 6 (the opening of Nocturne No. 7) how a basic tonal bass schema, $$\hat{1}$$–$$\hat{4}$$–$$\hat{5}$$, becomes blurred through $$^{6}_{3}$$ substitutions on both $$\hat{1}$$ and $$\hat{5}$$. To make things even more ambiguous, the bass pitches F$$\sharp$$ and G$$\sharp$$ lend themselves to interpretation in terms of the RO of B major rather than C$$\sharp$$ minor: this is shown in Example 12, which contains two actual chords and a hypothetical continuation according to the RO in B major.

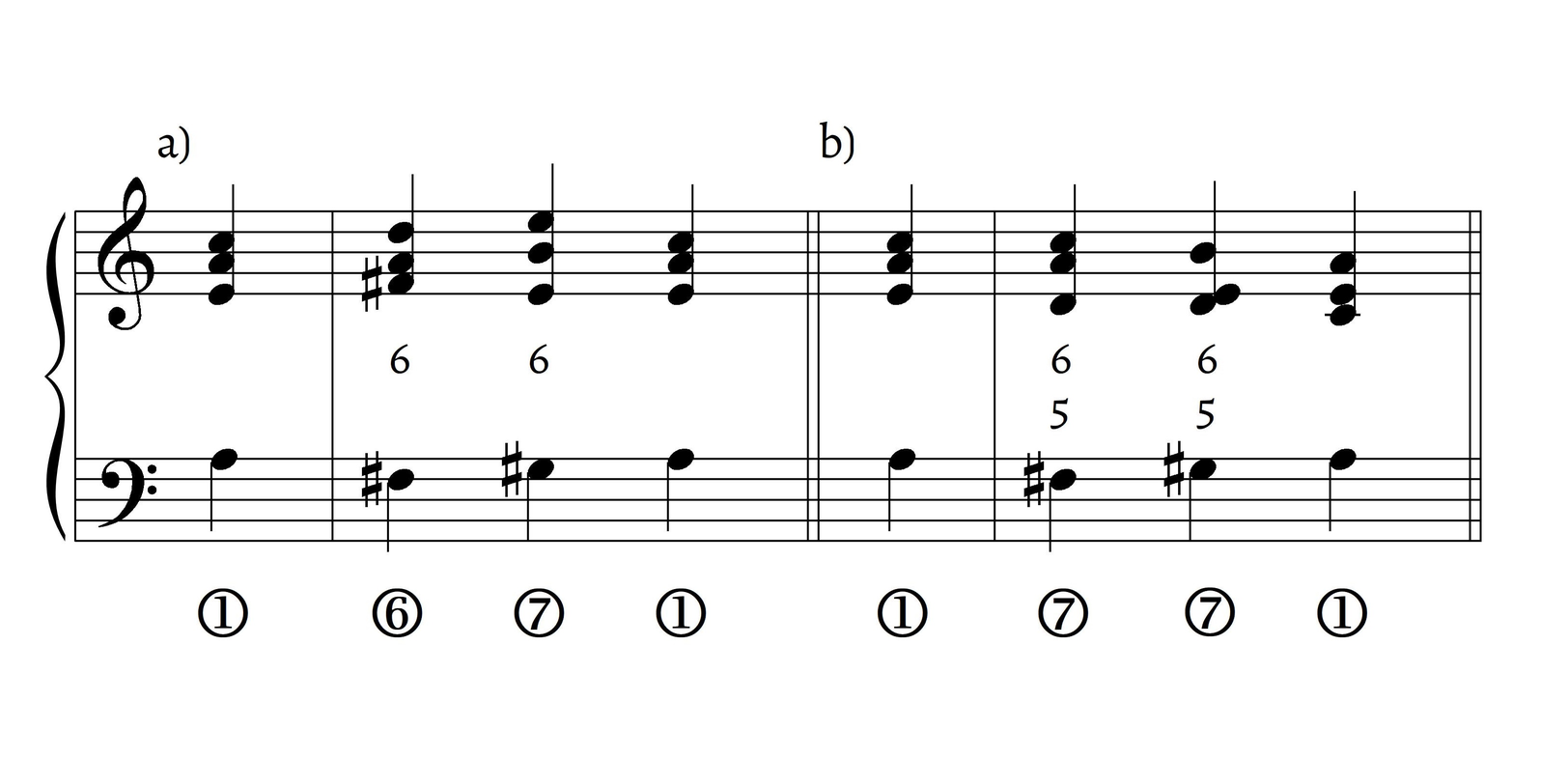
As an example of the traditional RO as a productive model for Fauré, let us take a look at the opening of the song “Puisque l’aube grandit” (Example 13a), the second song of the cycle La bonne chanson, op. 61. The initially established key, G major, gives way to B minor seamlessly: the sonority on $$\hat{5}$$ that opens m. 3 projects the relative “stability” of this scale degree through a triad—what might be called a “$$^{6}_{3}$$ substitution” of a root-position triad. One can easily reimagine the passage so as to resolve this substitution chord as a dominant in the original key of G major (see Example 13b). To use Agawu’s (1994) terms, this recomposition—like most of my recompositions in this article— shows a prospective implication that is subverted in the actual music. The $$^{6}_{3}$$ chord on D, however, also fits as a stable triad on $$\hat{3}$$ of the RO of B minor.¹⁷ In fact, as $$^{6}_{3}$$, it is an ideal fit above $$\hat{3}$$ in the traditional RO. The second chord of m. 3 also fits the identity of $$\hat{4}$$ in B minor, being a ø$$^{6}_{5}$$ chord. The original passage (Example 13a) thus proceeds through ascending $$\hat{3}$$–$$\hat{4}$$ in a traditional RO in B minor (see abstractions in Example 13c). The following descent through $$\hat{4}$$–$$\hat{3}$$–$$\hat{2}$$–($$\hat{5}$$)–$$\hat{1}$$ is close to a traditional descending RO: the only differences are that $$\hat{4}$$ maintains its “ascending” identity and that Fauré uses a $$\hat{2}$$-$$\hat{5}$$ motion (that does not ultimately resolve to $$\hat{1}$$) rather than a descending stepwise motion. In any case, $$\hat{4}$$ maintains its unstable quality, associated with a seventh chord.

I hear the second sonority of m. 3 in Example 13a (“A–C$$\sharp$$–E–G–B”) as a \hd$$^{6}_{5}$$ on E rather than as a ninth chord, since the note A resolves to B both in the voice and in the accompaniment. If we are to entertain A as a viable chord tone, it can also be understood as a dominant of D major, that is, V/V—a faint implication not realized. Either way, despite conflicting implications, Fauré’s harmonic building blocks are close to a traditional RO. By creating a $$^{6}_{3}$$ substitution on $$\hat{5}$$ of the original key, Fauré facilitates a reinterpretation of D as $$\hat{3}$$ in B minor: the game of fleeting tonal impressions can be conceptualized as a kind of position finding game along the RO.¹⁸

5. Analysis and Recomposition Vignette (i): Fantasy for Flute and Piano, op. 79

Like “Puisque l’aube grandit,” the opening of the Fantasy for Flute and Piano, op. 79 (Example 14a) also exemplifies the utility of the RO as a conceptual and practical model. To use Agawu’s terms again, my successive recompositions in Examples 14b–e reflect prospective implications that are not realized in the original piece. The fantasy starts with an almost traditional RO ascent through the first four scale degrees of E minor. In m. 3, the flute’s “passing” F$$\sharp$$ implies a traditional ii$$^{6}_{5}$$ sonority, while the piano’s IV⁷ is a slight variant that nevertheless maintains the qualitative distinction between stable scale degrees (matched with triads) and unstable ones (matched with seventh chords). M. 4 represents a traditional descending $$\hat{4}$$–$$\hat{3}$$ segment in E minor, at least as far as the piano part is concerned. The end of m. 4 brings about a conflict between the flute and piano: if the flute had its way (given its F$$\natural$$ inflection), the piano would harmonize the bass G with a $$^{\sharp4}_{2}$$, shifting to a traditional descending RO segment in D minor, followed by the actual $$^{6}_{3}$$ on F in m. 5, which indeed fits into the RO of D minor.¹⁹ Mm. 5–6 interpret the bass notes F–A–D as $$\hat{3}$$–$$\hat{5}$$–$$\hat{1}$$ in D minor. M. 6 is ambiguous in terms of its prospective implications: one possibility, actually realized in the music, is that this measure is locally in A minor; another option, realized in the recomposition of Example 14b, is a shift toward F major, such that $$^{6}_{3}$$ on the bass C as $$\hat{5}$$ is a $$^{6}_{3}$$ substitution. Fauré, however, seems to interpret the A-minor triad of the downbeat of m. 7 as a subdominant of the upcoming E minor—an implication that is also quickly subverted. (Needless to say, by invoking a “subdominant” function I am directly invoking an explanatory model other than the RO, which brings my work closer to conventional harmonic analysis in this case and others.) Example 14c expands upon the E-minor potential of mm. 7–8: bass F$$\sharp$$–G–A are taken as $$\hat{2}$$–$$\hat{3}$$–$$\hat{4}$$ in E minor. Though not a traditional RO harmonization, it maintains the qualitative distinction between triads and seventh chords.

A similar succession of $$\hat{2}$$–$$\hat{3}$$–$$\hat{4}$$, now respective to A minor, is realized in Example 14d: the unstable sonority on the bass B₂ in the original m. 6 (Example 14a) is thus interpreted here as implying $$\hat{2}$$ in A minor and resolves accordingly. Much like the original passage, which plays extensively on the lower pentachord of the RO, my recompositions explore possible prospective implications not realized.

Example 14e takes the potential implication of hearing the original opening sonority of m. 8 (see Example 14a above) as a $$^{6}_{3}$$ substitution on $$\hat{5}$$ in C major. This is followed by an attempt to reimagine fast-paced shifts that are in line with the language of the original piece: C is immediately reinterpreted upon resolution as $$\hat{5}$$ of F major, leading to a traditional $$\hat{5}$$–$$\hat{4}$$–$$\hat{3}$$ descending RO segment in mm. 9–10. The reinterpretation of the bass note A (m. 10) from $$\hat{3}$$ to $$\hat{4}$$ is achieved by changing the triadic $$^{6}_{3}$$ sonority to a ø$$^{6}_{5}$$ at the end of m. 10, that is, $$\hat{4}$$ in the RO of E minor whose identity is clarified through the ø$$^{6}_{5}$$ sonority; this plagal cadential formula is inspired by the original fantasy. Both the original excerpt and my reimaginings in this vignette extensively explore the pattern of stable and unstable scale degrees within the lower pentachord of the RO: fleeting tonal impressions are conceptualized based on positions within the RO, exploring paths not realized in the composer’s style through this traditional model.

6. Further Short Examples for the RO

“Le jardin de Dolly,” the third piece from the suite Dolly, op. 56,opens in a deceptively simple manner (Example 15a). Let us start unpacking it at m. 4: the dom$$^{6}_{5}$$ sonority on the bass note C$$\sharp$$ implies a resolution within D major given its presumptive identity as $$\hat{7}$$, which is strongly supported by the melody in this measure: this is reimagined in the recomposition of Example 15b.

At the outset of m. 3, E is harmonized with $$^{6}_{5}$$, suggesting that it shifts its identity from $$\hat{1}$$ in the home key to become $$\hat{4}$$ in B major.However, the following half-diminished sonority and $$^{6}_{5}$$ on C$$\sharp$$ suggests the possibility of hearing the latter sonority as $$\hat{4}$$ in G$$\sharp$$ minor, not only as vii$$^{6}_{5}$$ of B major. Moreover, the $$^{6}_{3}$$ on D$$\sharp$$ in the final beat of m. 3 might be a $$^{6}_{3}$$ substitution on $$\hat{5}$$ of G$$\sharp$$ minor. In other words, the combinations of chordal qualities and inversions again create a kind of position finding game along the RO. The G$$\sharp$$-minor hearing is realized in Example 15c.

In the actual piece (Example 15a), Fauré’s C$$\sharp$$–D$$\sharp$$ segment in m. 3 is a slight variant of the RO in B major, whereas m. 4 has a traditional RO segment in E major/minor with a (modal-mixture-inflected) $$^{6}_{3}$$ substitution on $$\hat{5}$$. A reduction of the original m. 4 along with a derivation from RO harmonization of bass $$\hat{5}$$–$$\hat{6}$$–$$\hat{7}$$ is given in Example 15d.

When the ascending RO segment $$\hat{6}$$–$$\hat{7}$$–$$\hat{1}$$ in minor is harmonized such that $$\hat{6}$$ carries $$^{6}_{5}$$, both $$\hat{6}$$ and $$\hat{7}$$ carry a dom$$^{6}_{5}$$ chordal quality (cf. Example 8b above). This creates a practical-conceptual dilemma captured by Holtmeier (2011, after Förster 1823, see Example 16): when bass $$\hat{6}$$ is harmonized with a dom$$^{6}_{5}$$, it might be construed as $$\hat{7}$$ of the key of VII due to associations between bass figures, chord qualities, and bass scale degrees. Emanuel Aloys Förster’s practical-analytical dilemma is based on the same key finding or position finding game that Fauré plays: chordal qualities contextually define tonal impressions, which can be conceptualized as bass positions along the RO. By marking the dom$$^{6}_{5}$$ sonority on F$$\sharp$$ as “$$\hat{7}$$,” Förster indicates a tonal implication, the significance of which will become clearer in the following two analyses.

              Let us move to Nocturne No. 4, op. 36 (Example 17a): after starting in E$$\flat$$ major, the opening sonority of m. 2 strongly implies the key of C minor: a ø$$^{6}_{5}$$ on what turns out to be $$\hat{4}$$ leads to a Fauré-style plagal cadence in C minor. Mm. 3–5 have rapid tonal shifts to implied G minor and F major. As in Holtmeier and Förster’s dilemma, Fauré exploits the ambiguity of a dom$$^{6}_{5}$$ sonority: as the recomposition of Example 17b shows, mm. 4–5 could well have led to B$$\flat$$ major, as implied by the dom$$^{6}_{5}$$ on A$$\natural$$ and by the right-hand melody. Indeed, the most obvious implication in context of the melody of m. 5, G₅–F₅–E$$\flat$$₅–D₅, is B$$\flat$$ major. By reinterpreting the sonority on bass note A$$\natural$$ as $$\hat{6}$$ in an ascending RO of C minor, Fauré continues the game of fleeting tonal impressions.

Before leaving the original excerpt (Example 17a), I would like to note that the dom$$^{4}_{2}$$ sonority in m. 8 brings to mind Harrison’s (1994) harmonic dualism and Pau’s (2016) application of dualism to Fauré and Duparc. The strongest prospective implication of this chord is to resolve as V$$^{4}_{2}$$ in E$$\flat$$ major; in the actual music, it precedes the dominant of C minor. In Harrison’s (1994) terms, we can think of the competition between these implications as that between an E$$\flat$$-major dominant functional agent ($$\hat{7}$$) in the soprano and a C-minor subdominant functional agent in the bass $$\hat{\flat6}$$: according to Harrison, functional agents are  “unequivocal communicators of their function” (1994, 49). Thus, this mysterious dom$$^{4}_{2}$$ does not lead to a dominant-tonic discharge in E$$\flat$$ major ($$\hat{7}$$–$$\hat{1}$$) as one might initially expect, but rather to a subdominant-dominant discharge in C minor ($$\hat{\flat6}$$–$$sd{5}$$).²⁰ If my approach is eclectic, it simply indicates the complexity of the subject matter and the need for multiple explanatory models in engaging the composer’s harmony.²¹

The opening of Fauré’s Nocturne No. 6 in D$$\flat$$ Major, op. 63 (Example 18a) is among the most striking passages in his oeuvre. The scale degrees in mm. 1–3 create an exceedingly traditional tonal trajectory: $$\hat{1}$$–$$\hat{5}$$–$$\hat{6}$$–$$\hat{7}$$–$$\hat{1}$$–$$\hat{4}$$–$$\hat{5}$$–$$\hat{1}$$. As discussed above after Caron, this formulaic bass has simple tonal implications, which are clouded by Fauré’s disorienting upper voices.

              The opening sonority of m. 1 is already a $$^{6}_{3}$$ substitution respective to this bass frame: this means that the basic $$\hat{1}$$–$$\hat{5}$$ tonal relation across the bar line of mm. 0–1 is already ambiguous, failing to establish the home key clearly. The half-diminished on C at the end of m. 1 is also ambiguous: while it maintains the key-defining tritone of the original key of D$$\flat$$ major, it also implies a potential shift to B$$\flat$$ minor, a prospective implication realized in the recomposition of Example 18b.

M. 4 (see Example 18a) brings about a shift to E$$\flat$$ minor (key of ii), although the dom7 quality of the opening chord may well be understood at first in the home key based on the preceding resolution to the tonic at the end of m. 3. This revisits Förster and Holtmeier’s ambiguity (Example 16): the opening chord is heard prospectively as $$^{6}_{5}$$ over $$\hat{7}$$ in the original key, but it is reinterpreted as a $$^{6}_{5}$$ sonority on $$\hat{6}$$ in the RO model of E$$\flat$$ minor. The characteristic $$\hat{6}$$–$$\hat{7}$$–$$\hat{1}$$ RO—a truncated tetrachord—surprisingly ends not on a $$^{5}_{3}$$ chord on E$$\flat$$ but rather on a $$^{6}_{3}$$ substitution (see Example 18a, m. 4). Example 18c shows how m. 4 would sound with the more expected $$^{5}_{3}$$ on E$$\flat$$. In reality (Example 18a), Fauré moves to a $$^{6}_{3}$$ substitution on $$\hat{5}$$ of the home key (m. 5) before resolving contrapuntally to a conventional (and tonally clearer) dom7 sonority. The diatonic motion $$\hat{2}$$–$$\hat{5}$$ across the bar line between m. 4 and m. 5 is thus matched with two $$^{6}_{3}$$ sonorities. Again, Fauré takes a simple tonal bass schema and matches it with disorienting upper-voice sonorities.

M. 6 (see Example 18a) revisits the $$\hat{6}$$–$$\hat{7}$$–$$\hat{1}$$ RO segment of E$$\flat$$ minor, but this time the $$^{6}_{3}$$ on $$\hat{1}$$ is taken at face value: it is reinterpreted as a subdominant of G$$\flat$$ major.²² The V⁹ (dom9) chordal quality at the opening of m. 7 strongly suggests G$$\flat$$ major as the new tonic. The following B$$\flat\flat$$ $$^{6}_{3}$$ chord, too, may be conceptualized as a mixture $$^{6}_{3}$$ substitution on $$\hat{5}$$ respective to G$$\flat$$ major/minor: Example 18d explores this subverted prospective implication in recomposition through a phrase that shifts from G$$\flat$$ major to the home key of D$$\flat$$ major (mm. 7–10). Of course, a mixture $$^{6}_{3}$$ substitution on $$\hat{5}$$ is identical to the sonority on B in m. 4 of “Le jardin de Dolly,” seen in Example 15a above. (In the original—see Example 18a—the mixture $$^{6}_{3}$$ substitution on D$$\flat$$ is also taken at face value and leads to a tonicization of A major=B$$\flat\flat$$ major). If the recomposition of Example 18d is less successful than others, it is perhaps because it would fit better into an earlier Fauré work such as the Violin Sonata No. 1 in A Major, op. 13, rather than to the sound world of Nocturne No. 6. Nevertheless, it was crafted as an attempt to emulate the composer’s style. This nocturne opening captures two of my main points: 1) certain ambiguous harmonic progressions in Fauré’s music can be conceptualized as manipulations of RO segments, which can lead productively to the reimagining of unfulfilled prospective implications in recomposition; 2) simple bass schemata are matched with tonally disorienting upper-voice structures, often $$^{6}_{3}$$ substitutions.

To end this lengthy discussion, let us return to the passage from the “Libera me” of Fauré’s Requiem, op. 48 and examine how the original passage—as well as a couple of compositional reimaginings—can be conceptualized in terms of the RO. The original (Example 19a) ends on a Fauré-style plagal cadence (mm. 16–17).

The entrance of a $$^{6}_{5}$$ chord on G in the original passage (Example 19a, m. 12) prospectively suggests that the following bass A in m. 13 might be $$\hat{5}$$ of D minor. This is a plausible interpretation given Fauré’s fondness for $$^{6}_{3}$$ substitutions: F⁶ could well have resolved to the D-minor tonic, directly or after contrapuntal motion to a root-position chord. The D-minor implication, however, becomes difficult to entertain once the half-diminished seventh sonority on B$$\natural$$ enters in m. 14: its tonal implication is likely $$\sharp\hat{4}$$ in F major or $$\hat{2}$$ in A minor. In retrospect, however, the bass notes A–B–C–D (mm. 13–16) turn out to be RO segment $$\hat{1}$$–$$\hat{2}$$–$$\hat{3}$$–$$\hat{4}$$ in A minor, maintaining a qualitative difference between stable and unstable scale degrees.

Example 19b shows one of the paths not taken based on the prospective implications of the half-diminished sonority: B$$\natural$$ in m. 14 is interpreted as $$\sharp\hat{4}$$ in F major, and C as $$\hat{5}$$ of F major carries first a $$^{6}_{3}$$ substitution, then resolves contrapuntally to a tonally clearer dom7 chord.²³

Example 19c realizes an additional implication: that the ø$$^{6}_{5}$$ in m. 12 could be $$\hat{4}$$ of D minor: now A in m. 13, which carries a $$^{6}_{3}$$, is taken to be $$\hat{5}$$ of D minor (i.e., a $$^{6}_{3}$$ substitution), making the preceding $$^{6}_{5}$$ chord into a typical RO sonority on $$\hat{4}$$. Though not my main focus—and though I do not currently have a good explanatory model for the composer’s pedal points—the fauxbourdon-like harmonies above the A pedal attempt to emulate the composer’s style.²⁴ This pedal point is necessary in order to maintain Fauré’s original phrase rhythm. The entrance of C$$\sharp$$ in m. 16 unambiguously clarifies the dominant quality of bass $$\hat{5}$$.

My lengthy discussion in this section of several passages representative of the composer’s usages suggests that the RO model can describe an aspect of the composer’s harmonic idiolect. RO segments realized and subverted are at the center of certain ambiguous passages even if Fauré’s usage is somewhat more abstract in comparison to the traditional model: matching non-traditional upper-voice sonorities to bass gambits across segments of the RO creates a degree of ambiguity. Yet recognizable elements—particular sonorities associated with specific scale degrees or the qualitative distinction between stable and unstable degrees—can help orient us in analysis and recomposition.   

7. Analysis and Recomposition Vignette (ii): “Introit & Kyrie” from the Requiem, op. 48

Richard Cohn (2012) discusses a passage from the “Introit & Kyrie” of the Requiem, which, in his view, is based on the fulcrum of an F–A–C$$\sharp$$ augmented triad. He writes about the score excerpt in his figure 3.8 (paraphrased in my graphic Example 20):

Like much of the d minor Introit/Kyrie movement from which it is drawn, this passage is animated by the tonic’s relationship to an F major triad that consistently functions as dominant. The melodic fulcrum of this relationship is the C$$\sharp$$ that mediates between C and D, and hence the harmonic fulcrum is the FAC$$\sharp$$ augmented triad that appears at m. 60, just prior to the cadence. This same augmented triad, spelled variously, also appears three times in the interior of the phrase, each time as the second component of a two-chord unit whose first component is a consonant triad: F major at m. 52, f$$\sharp$$ minor at m. 54, and b$$\flat$$ minor at m. 56. (2012, 54–55)

A “$$^{6}_{3}$$ substitution on $$\hat{5}$$” in the terms of my article is, of course, a different approach to describing Cohn’s F-major triad functioning “as dominant.” Cohn observes that “there is no consistent diatonic explanation that accounts for the simultaneous presence of this particular group of triads in a single phrase. What draws them together is their shared status as single semitonal displacements of FAC$$\sharp$$” (2012, 55). In contrast with Cohn’s chromatic and symmetrical lens, I will argue that the diatonic and asymmetrical RO offers an additional viewpoint on this enigmatic passage.

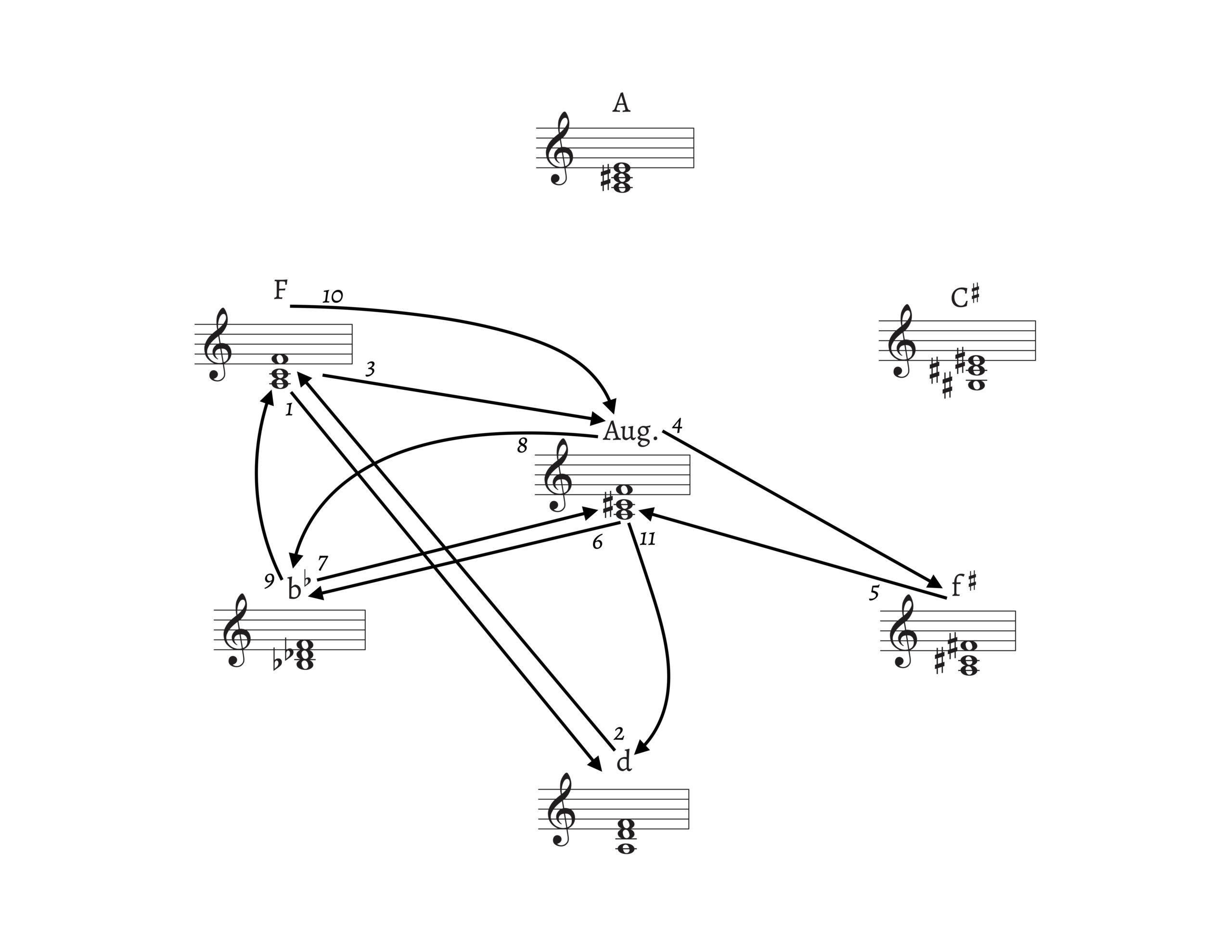
Cohn’s explanation is insightful in that it provides a compact chromatic account of a progression that is difficult to conceptualize from a diatonic or functional viewpoint: the sonorities in this passage all involve semitonal displacement of the A–C$$\sharp$$–F augmented triad. In addition, his analysis is also effective because the exaudi passage is the highpoint of the “Introit & Kyrie”: the F$$\sharp$$₅ in m. 54 is the highest soprano note in the entire movement, exceeding the vocal range that generally reaches only to F₅. Cohn refers to the F$$\sharp$$-minor triad as “intractable” and wonders if it functions as iii of D major, which is not present in this movement. However, in so doing, he ignores an associated passage, mm. 25–28 of the “In Paradisum” movement (not shown) in which a $$^{6}_{3}$$ substitution on $$\hat{5}$$ oscillates between major and minor triad qualities.²⁵ Thus, a “dominant-functioning” or $$^{6}_{3}$$-carrying $$\hat{5}$$ is involved in long-range connections: the exaudi plea is fulfilled in paradisum.

Though Cohn’s observations are insightful, I would like to offer an alternative interpretation. Example 21a reduces the exaudi passage while retaining Fauré’s oscillating bass line. Crucially, in m. 56 and m. 58, the bass line adds a G, which underlies Cohn’s B$$\flat$$-minor triad, one of the members of his Weitzmann region. Cohn’s omission of the G allows him to focus on interesting triadic relationships, yet it seems preferable to account for this pitch rather than ignore it. The G turns the B$$\flat$$-minor triad into a half-diminished seventh: in mm. 58–59, the combination of a Gø seventh chord and an F$$^{6}_{3}$$ chord creates a strong tonal implication of F major. Example 21b recomposes the passage, showing the potential of the Gø to participate as an implied $$\hat{2}$$ respective to F major. The recomposition (mm. 58–59) tips the balance momentarily in favor of F major rather than D minor. Recomposed mm. 59–60 draw on Fauré’s play between F–A–C and F–A–C$$\sharp$$ triads, the latter of which clearly leads the way back to the main tonal center, D minor.  

Example 21a. Reduction and analysis of “Introit & Kyrie” from the Requiem, Op. 48, mm. 50–61

Examples 21a and 21b suggest that a diatonic, RO-oriented account of this passage is viable, complementing Cohn’s insights about the central augmented triad. The usefulness of annotating bass scale degrees respective to the local tonic is clear in this context: though the upper voices are unconventional, the bass segments can provide tonal orientation.

The exaudi climactic passage should also be considered in conjunction with the harmonically dense interlude reproduced in Example 22a, which provides a further opportunity to explore the potential of the RO for reimagining harmonic paths in this movement.

After a clear $$\hat{6}$$–$$\hat{7}$$–$$\hat{1}$$ RO segment in A minor in m. 38, the G°⁷, A augmented, and $$^{6}_{5}$$ on B$$\flat$$ in the following measure are more disorienting. If only G in m. 39 carried G–B$$\flat$$–D–E, it would have implied a return to D minor through a clear RO $$\hat{4}$$ identity. In such a case, the augmented triad on A would be a $$^{6}_{3}$$ substitution containing a leading tone, which conforms to Fauré’s usage in this movement. This is realized in the recomposition of Example 22b, which also shows how a pedal point on A could lead smoothly to a cadence in the principal tonal center of D minor.

Had G in m. 39 carried G–B$$\flat$$–D$$\flat$$–F, a shift to F major would have been implied. The $$^{6}_{5}$$ on B$$\flat$$ (original m. 39, Example 22a) indeed suggests $$\hat{4}$$ in the RO of F major. The perfectly symmetrical \dim7 quality in m. 39 could have been clarified—and rendered more diatonic—through a slight displacement. Example 22c tilts the sonority in the direction of F major. The recomposition of Example 22c also turns decisively toward F major at its end. Admittedly, this ending might fit better into the sound world of the simpler Messe basse than to the Requiem, but it is still an attempt at style-bound recomposition.

This interlude demonstrates how modified segments of the RO can participate in speculating on the more diatonic properties of this movement and guide us toward creativity in a historical style. Though Fauré certainly participated in romantic explorations of the triad’s second nature (Cohn 2012), the complex harmony of this movement can be conceptualized and explored through the more diatonic lens of the RO, complementing Cohn’s chromatic approach.

8. Fauré-izing Debussy, Listening to Satie through Fauré

BaileyShea’s (2007) recomposed mashup of different settings of one of Johann Wolfgang von Goethe’s Mignon poems, “Nur wer die Sehnsucht kennt,” reveals interesting motivic connections between the pieces and provides a vivid demonstration of intertextual links and influences between the settings: his creative exercise thus acts as a commentary on the pieces that is more visceral than what could be accomplished using prose and analytical examples alone. In this final, brief vignette, I would like to sketch some of the lines connecting Fauré to Debussy. I will do so by recasting small portions of Debussy’s “Clair de lune” from the Suite bergamasque into the style of Fauré based (inter alia) on the considerations of the present article. I will also reflect on listening to one of Satie’s well-known Gymnopédies through the sieve of Fauré’s harmony. In both cases, iconic pieces are heard here in a slightly different way through Fauré’s prism—without trying to ascertain lines of influence.

Example 23a hybridizes the opening gestures of Debussy’s “Clair de lune” and the style of Fauré.²⁶ I have used RO segments both in the home key and in the key of III (mm. 1–4 and mm. 9–12, respectively). This is somewhat inspired by the tonal ambiguity of the first variation from Fauré’s exquisite Theme and Variations in C$$\sharp$$ Minor, op. 73 (not shown): this variation takes the pitches $$\hat{5}$$–$$\hat{6}$$–$$\hat{7}$$–$$\hat{3}$$–$$\hat{4}$$–$$\hat{5}$$–$$\hat{1}$$ (G$$\sharp$$–A–B–E–F$$\sharp$$–G$$\sharp$$–C$$\sharp$$ (theme, mm. 2–3), and turns them into a bass line so that these melodic scale degrees, now in the bass, are reinterpreted as $$\hat{3}$$–$$\hat{4}$$–$$\hat{5}$$–$$\hat{1}$$ in E major then C$$\sharp$$ minor (var. 1, mm. 2–3). I have also used sequence models in this passage: in mm. 5–7, a Fauré-style, fake-fauxbourdon sequence with parallel $$^{4}_{3}$$ chords is used; in mm. 13–14, an ascending 5–6 sequence model already sounds closer to the style of Debussy. In recasting this passage (Debussy’s original mm. 1–14), I had to deviate quite a bit from the original gestures in an attempt to emulate Fauré’s style; nevertheless, the general gestures and contour have been maintained, especially in the reimagined mm. 1–12 (roughly equivalent to Debussy’s original mm. 1–10). When we reimagine Debussy through Fauré’s harmony, events like Debussy’s $$^{6}_{5}$$ on G$$\flat$$ in m. 10 and m. 12 can be thought of in terms of the RO mold. My distant reimagining relies more on intuition than on explicit theorizing: I have reported here on the musical structures that I explicitly thought about, but this surely does not articulate all factors involved.

Example 23b recasts the opening of Debussy’s striking passage starting in m. 27, which is adapted here as a non-traditional RO segment. The “wrong” $$^{4}_{2}$$ sonority on $$\hat{4}$$ sets up the two $$^{6}_{3}$$ substitutions of the second measure. Debussy’s iconic F$$\flat^{6}$$ sonority in m. 27 can thus be conceptualized as a Fauré-style mixture $$^{6}_{3}$$ substitution. The mashup fragments offered here hint at some of the potentials of analysis and model composition to complement one another: the project of reimagining fragments of one of Debussy’s early pieces through Fauré was based partially on an explicit analytical approach to Fauré’s music and partially on intuitions that are more difficult to articulate, revealing some experiential connections between the two composers.

Finally, Example 24 reproduces an excerpt from Satie’s Gymnopédie no. 2 in which the lens of Fauré’s harmony can also potentially elucidate some unusual events. Satie uses Fauré-like pedal points with upper-voice fauxbourdon variants (mm. 18–23, 31–35), which resolve—in a “dominant-tonic” fashion—into local tonics on B$$\flat$$ with a $$^{6}_{3}$$ substitution in m. 24 and m. 36. Again, an iconic piece, which is better-known than many of Fauré’s works, can be experienced through the present analytical and recompositional perspective.

Conclusion

This article has explored Fauré’s harmony through analysis and recomposition. I have used these activities in support of an analytical claim about Fauré’s harmonic usage, as well as a broader proposal regarding the possible role of recomposition in music theory and analysis (and beyond). I have demonstrated that the traditional model of the RO (with modifications) can explain some of the fast-changing tonal impressions in Fauré’s harmony. His manipulations of the RO seem to be part of a broader tendency to use conventional bass schemata and match them with non-traditional upper-voice sonorities. In particular, unpacking ambiguities involving $$^{6}_{3}$$ and $$^{5}_{3}$$ sonorities can help us to decipher Fauré’s enigmatic harmonic surface. As a conceptual model and latent view of tonality, the RO provides us a different view of Fauré’s famously fleeting tonal impressions: specific sonorities and inversions orient us to a local tonal center. At the same time, the approach taken here is not purist or historicist—I have considered intersections with recent analytical literature on harmonic ambiguity and have showed how the model is used abstractly, not literally. Moreover, I must emphasize again that the RO explains only parts of Fauré’s language but does not give a comprehensive account of his harmonic usage.

My second claim—or, rather, proposal—is that analysis and style-bound recomposition can support one another. By explicitly trying to emulate Fauré’s style, one can gain a more intimate understanding of the composer’s idiolect. Creating in historical styles is also a good way to test the accuracy of our analytical tools in describing historical styles: style-bound recomposition (or model composition more generally) requires understanding the idiom beyond labelling systems. While I do not claim that my recompositions are precise emulations of the composer’s style, I believe that through immersion and model composition we can actively test our evolving analytical understanding. Recomposition is thus no longer an analytical straw man, but rather an opportunity to explore from within the back-and-forth between analysis and creativity in a historical style. 

Acknowledgement

The author and editorial team would like to thank Shangru Du for recording the article’s many recompositions and bringing them to life in the journal’s open-access format.

---

References

Agawu, Kofi. 1994. “Ambiguity in Tonal Music: A Preliminary Study.” In Theory, Analysis and Meaning in Music, edited by Anthony Pople, 86–107. Cambridge: Cambridge University Press.

Aziz, Andrew. 2015. “Recomposition and the Sonata Theory Learning Laboratory.” Journal of Music Theory Pedagogy Online 5. https://drive.google.com/file/d/0B0ZI8di-pEDvejU4OFhDSnhZZDQ/view?resourcekey=0-0tMZ6Gruud-KoJC9p2tkKA.

BaileyShea, Matthew K. “Filleted Mignon: A New Recipe for Analysis and Recomposition.” Music Theory Online 13 (4). https://mtosmt.org/issues/mto.07.13.4/mto.07.13.4.baileyshea.php.

Blättler, Damian J. 2017. “A Voicing-Based Model for Additive Harmony.” Music Theory  Online 23 (3). https://mtosmt.org/issues/mto.17.23.3/mto.17.23.3.blattler.html.

Browne, Richmond. 1981. “Tonal Implications of the Diatonic Set.” In Theory Only 5 (6/7): 3–21.

Byros, Vasili. 2009. “Foundations of Tonality as Situated Cognition, 1730–1830: An Enquiry into the Culture and Cognition of Eighteenth-Century Tonality with Beethoven’s ‘Eroica’ Symphony as a Case Study.” PhD diss., Yale University.

———. 2012. “Meyer’s Anvil: Revisiting the Schema Concept.” Music Analysis 31 (3): 273–346.

———. 2015. “Prelude on a Partimento: Invention in the Compositional Pedagogy of the German States in the Time of J. S. Bach.” Music Theory Online 21 (3). https://mtosmt.org/issues/mto.15.21.3/mto.15.21.3.byros.html.

Cafiero, Rosa. 2007. “The Early Reception of Neapolitan Partimento Theory in France: A Survey.” Journal of Music Theory 51 (1): 137–159.

Caron, Sylvain. 2002. “Écriture tonale et perspectives nouvelles de l’harmonie fauréenne.” Canadian University Music Review/Revue de musique des universités canadiennes 22 (2): 48–76.

Chailley, Jacques. 1982. “Momigny, Maleden et l’école Niedermeyer.” In Logos musicae: Festschrift für Albert Palm, edited by Rüdiger Görner, 8–18. Wiesbaden: Steiner.

Choron, Alexandre-Étienne, and Vincenzo Fiocchi. 1804. Principes d’accompagnement des écoles d’Italie. Paris: Imbault.

Christensen, Thomas, 1992. “The Règle de l’octave in Thorough-Bass Theory and Practice.” Acta Musicologica 64 (2): 91–117.

———. 2019. Stories of Tonality in the Age of François-Joseph Fétis. Chicago: University of Chicago Press.

Cohn, Richard. 2012. Audacious Euphony: Chromatic Harmony and the Triad’s Second Nature. New York: Oxford University Press.

Cook, Nicholas. 1987. A Guide to Musical Analysis. London: Dent.

Damschroder, David. 2008. Thinking about Harmony: Historical Perspectives on Analysis. Cambridge: Cambridge University Press.

Eng, Sher Ling Clare. 2012. “Motif and Closure in Twentieth-Century Music: Bartók, Britten, and Fauré.” PhD diss., Yale University.

Förster, Emanuel Aloys. 1823. Anleitung zum Generalbaß (2. Auflage). Vienna: Artaria.

Gjerdingen, Robert O. 2007. Music in the Galant Style. New York: Oxford University Press.

———. 2020. Child Composers in the Old Conservatories: How Orphans Became Elite Musicians. New York: Oxford University Press.

———. 2021. “Fauré as Student and Teacher of Harmony.” In Fauré Studies, edited by Carlo Caballero and Stephen Rumph, 59–79. Cambridge: Cambridge University Press.

Greer, Taylor. 1991. “Modal Sensibility in Gabriel Fauré’s Harmonic Language.” Theory and Practice 16: 127–142.

Hannaford, Marc. 2019. “One Line, Many Views: Perspectives on Music Theory, Composition, and Improvisation through the Work of Muhal Richard Abrams.” PhD diss., Columbia University.

———. 2020. “Recomposing the Referent: An Ecological Perspective.” Paper presented at the Society for Music Theory’s 43rd Annual Conference, Virtual, November 8, 2020.

Harrison, Daniel. 1994. Harmonic Function in Chromatic Music: A Renewed Dualist Theory and an Account of its Precedents. Chicago: University of Chicago Press.

Hepokoski, James, and Warren Darcy. 2006. Elements of Sonata Theory: Norms, Types, and Deformations in the Late-Eighteenth-Century Sonata. New York: Oxford University Press.

Hoag, Melissa. 2013. “Hearing ‘What Might Have Been’: Using Recomposition to Foster Music Appreciation in the Theory Classroom.” Journal of Music Theory Pedagogy 27: 47–70.

Hogrefe, Eric. 2020. “Recomposing Phrase Structure.” In The Routledge Companion to Music Theory Pedagogy, edited by Leigh VanHandel, 279–283. New York: Routledge.

Holtmeier, Ludwig. 2002. “Reconstructing Mozart.” Translated by Richard Evans. Music Analysis 21 (3): 307–325.

———. 2011. “Funktionale Mehrdeutigkeit, Tonalität und arabische Stufen: Überlegungen zu einer Reform der harmonischen Analyse.” Zeitschrift der Gesellschaft für Musiktheorie 8 (3): 465–487.

Huron, David. 2001. “Tone and Voice: A Derivation of the Rules of Voice-Leading from Perceptual Principles.” Music Perception 19 (1): 1–64.

———. 2006. Sweet Anticipation: Music and the Psychology of Expectation. Cambridge, MA: MIT Press.

Hyer, Brian. 1996. “Second Immediacies in the Eroica.” In Music Theory in the Age of Romanticism, edited by Ian Bent, 77–104. Cambridge: Cambridge University Press.

Jelensperger, Daniel. 1830. L’harmonie au commencement du 19me siècle et méthode pour l’étudier. Paris: Zetter.

Johansen, Ken. 1999. “Gabriel Fauré: Un art de l’équivoque.” Revue de musicologie 85 (1): 63–96.

Johnson, Shersten. 2014. “Recomposition as Low-Stakes Analysis.” Engaging Students 2. http://flipcamp.org/engagingstudents2/essays/johnson.html.

Kidd, James C. 1973. “Louis Niedermeyer’s System for Gregorian Chant Accompaniment as a Compositional Source for Gabriel Fauré.” PhD diss., University of Chicago.

Klorman, Edward. 2016. Mozart’s Music of Friends: Social Interplay in the Chamber Works. Cambridge: Cambridge University Press.

Krumhansl, Carol K. 1990. Cognitive Foundations of Musical Pitch. New York: Oxford University Press.

Lefèvre, Gustave. 1889. Traité d’harmonie. Paris: L’École [de musique classique fondée par L. Niedermeyer].  

Lester, Joel. 1992. Compositional Theory in the Eighteenth Century. Cambridge, MA: Harvard University Press.

Lewin, David. 1986. “Music Theory, Phenomenology, and Modes of Perception.” Music Perception 3 (4): 327–392.

Mavromatis, Panayotis. 2012. “Exploring the Rhythm of the Palestrina Style: A Case Study in Probabilistic Grammar Induction.” Journal of Music Theory 56 (2): 169–223.

Meyer, Leonard B. 1989. Style and Music: Theory, History, and Ideology. Philadelphia: University of Pennsylvania Press.

Moreno, Jairo. 2003. “Subjectivity, Interpretation, and Irony in Gottfried Weber’s Analysis of Mozart’s ‘Dissonance’ Quartet.” Music Theory Spectrum 25 (1): 99–120.

Nectoux, Jean-Michel, ed. 1980. Gabriel Fauré: Correspondance. Paris: Flammarion.

——. 1991. Gabriel Fauré: A Musical Life. Translated by Roger Nichols. Cambridge: Cambridge University Press.

Niedermeyer, Louis, and Joseph d’Ortigue. 1859. Traité théorique et pratique de l’accompagnement du plain-chant (Deuxième tirage). Paris: Repos.

O’Hara, William E. 2017. “The Art of Recomposition: Creativity, Aesthetics, and Music Theory.” PhD diss., Harvard University.

Pau, Andrew. 2016. “Plagal Systems in the Songs of Fauré and Duparc.” Theory and Practice 41: 81–111.

Phillips, Edward. 1993. “Smoke, Mirrors and Prisms: Tonal Contradiction in Fauré.” Music Analysis 12 (1): 3–24.

Rabinovitch, Gilad. 2018. “Daniel Jelensperger’s (1830) Views on Harmonic Impressions, Key Finding, and Statistical Learning.” Theoria 25: 35–62.

———. 2020. “Reimagining Historical Improvisation: An Analysis of Robert Levin’s Fantasy on Themes by W. A. Mozart, October 29, 2012.” Music Theory Online 26 (2). https://mtosmt.org/issues/mto.20.26.2/mto.20.26.2.rabinovitch.html.

Rings, Steven. 2011. Tonality and Transformation. New York: Oxford University Press.

———. 2021. “Jankélévitch, Fauré, and the Thirteenth Nocturne.” In Fauré Studies, edited by Carlo Caballero and Stephen Rumph, 233–255. Cambridge: Cambridge University Press.

Rogers, Nancy. 2013. “Modernizing the Minuet Composition Project.” Journal of Music Theory Pedagogy 27: 71–110.

Sanguinetti, Giorgio. 2012. The Art of Partimento: History, Theory, and Practice. New York: Oxford University Press.

Saslaw, Janna. 1990–1991. “Gottfried Weber and Multiple Meaning.” Theoria 5: 74–103.

Schubert, Peter. 2008. Modal Counterpoint, Renaissance Style. New York: Oxford University Press.

———. 2011. “Global Perspective on Music Theory Pedagogy: Thinking in Music.” Journal of Music Theory Pedagogy 25: 217–233.

———. 2020. “Contrapunto Fugato: A First Step Toward Composing in the Mind.” Music Theory Spectrum 42 (2): 260–279.

Smith, Charles J. 1986. “The Functional Extravagance of Chromatic Chords.” Music Theory Spectrum 8: 94–139.

Smith, Peter H. 1997. “Brahms and Motivic 6/3 Chords.” Music Analysis 16 (2): 175–217.

———. 2000. “Outer-Voice Conflicts: Their Analytical Challenges and Artistic Consequences.” Journal of Music Theory 40 (1): 1–43.

Sobaskie, James. 1999. “Allusion in the Music of Gabriel Fauré.” In Regarding Fauré, edited by Tom Gordon, 163–206. Amsterdam: Gordon and Breach.

Tait, Robin. 1989. The Musical Language of Gabriel Fauré. Outstanding Dissertations in Music from British Universities. NY and London: Garland.

Terefenko, Dariusz. 2018. Jazz Theory: From Basic to Advanced. 2nd ed. New York and London: Routledge.

1. Though the context is considerably different, my usage of “in dialogue” follows Hepokoski and Darcy (2006).
2. Of course, the A-major quality of m. 17 makes it sound also like a dominant of the home key of D minor, yet this is a formulaic plagal cadence in the composer’s style. Regarding the Fauré-style cadence that can be described as ii$$^{6}_{5}$$–I, with or without a melodic lower neighbor $$\flat\hat{7}$$, see, e.g., Caron (2002, 56–57), Eng (2012, 177, figure 80), and Gjerdingen (2021, 75–77). Indeed, Caron refers to this cadence as “the so-called Fauré-style cadence” (in the original: “La cadence dite ‘à la Fauré’”). For a dualist derivation of this cadence, see Pau (2016, 84, example 2). To give just two examples for this type of cadence beyond those featured in my article, see m. 4 as well as the final cadence from Fauré’s “Sanctus” in his Messe basse and m. 3 of the Nocturne No. 12, in which a ii$$^{6}_{5}$$–i resolution at the end of a Romanesca sequence creates tonal clarity before an unusual bass $$\flat\hat{5}$$.
3. For an introduction to the RO, see Christensen (1992). See also Gjerdingen’s (2020, 306–309) discussion of the relevance of the RO to Ravel’s ways of conceptualizing the harmonies of one of his Valses nobles et sentimentales, and Gjerdingen (2021, esp. 63–65, 72–73) regarding the École Niedermeyer-Fauré-RO connection. These connections leave much to unpack and speculate on, and the present article represents one step in this process.
4. Scholars of a more formal orientation have already shown that pedagogical prescriptions for voice-leading or counterpoint capture underlying principles and regularities in musical styles. For instance, Huron (2001) discusses the connections between traditional principles of part-writing and research in music cognition; Mavromatis (2012) compares traditional pedagogies of Renaissance-style counterpoint with a formal probabilistic model that captures the rhythmic aspect of Palestrina’s works. Though my article is far from a formal corpus study of Fauré’s harmonic usage, I hope that it can be a step toward modeling the composer’s style—analytically, creatively, or in more systematic studies.
5. The value of (re)composition has also been explored in recent contributions to the pedagogy of music theory: see Hoag (2013), Rogers (2013), Johnson (2014), Aziz (2015), and Hogrefe (2020).
6. Of course, this observation is very much related to Rings’s functional reading of the passage (132, figure 3.17a)—my entry point here is simply that of bass scale-degree patterns rather than the various technologies that Rings uses.
7. Caron (2002, 64) argues that this passage should be explained as a combination of contrapuntal lines in motion rather than as a chord progression. While this observation has merit, I believe that the harmonic implications discussed by Rings are highly relevant to our experience.
8. Compare these notions to David Huron’s observation that “Wagner’s harmonic practice relies on those elements of Western music that are the most clichéd and so the most evocative. . . . In using cadential formulas like the German sixth followed by the tonic 6–4 followed by the dominant [Huron refers here to the resolution of a cadential 6-4 chord], Wagner regularly taps into second- and higher-order probabilities that would have been highly familiar to his nineteenth-century European audience. The phenomenal experiences evoked by Wagner’s music are closely linked to his use of statistical patterns of tendency, while avoiding the statistical patterns related to repose or closure” (2006, 338–339). Though Fauré’s harmonic surface often differs from Wagner’s, it similarly relies on tonal expectations associated with specific harmonic formulas and individual chordal qualities.
9. Compare this also to Harrison’s (1994, 66) statement that “A $$\hat{4}$$–$$\hat{1}$$ [bass] motion from a diminished $$^{4}_{3}$$ chord, for instance, clearly works out a plagal cadence,” as he demonstrates with an excerpt from Richard Strauss’s Piano Quartet, op. 13. I cannot do justice here to Harrison’s complex treatment of diminished seventh chords but would like to emphasize from my present angle the importance of this bass pattern for recognizing a salient plagal cadence.
10. On the adoption and considerable transformation of partimenti in the nineteenth century at the Paris Conservatory, see Cafiero (2007) and Gjerdingen (2020).
11. Kidd (1973). See also Tait (1989, chapter 2) for a discussion of Niedermeyer and d’Ortigue’s treatise.
12. Lefèvre’s treatise is also related to Gottfried Weber through a Weber-influenced treatise from the Paris Conservatory orbit, that of Daniel Jelensperger (1830). Lefèvre (1889, 15) maintains the rankings of root progressions proposed by Jelensperger (1830, 29) based on the latter’s corpus study on harmonic usage ca. 1780–1830. On Jelensperger’s treatise, see Damschroder (2008) and Rabinovitch (2018). On Gottfried Weber’s theories, see Saslaw (1990–1991) and Moreno (2003).
13. On Fauré’s partimento lineage, see Gjerdingen (2021, esp. 62–63).
14. Terefenko (2018 workbook, 209–211) contains extravagant Fauré-style progressions, including what he refers to as diatonic and chromatic règle [de l’octave] or RO in the composer’s style. While Terefenko’s models are highly idiomatic, I believe that there is also value in conceptualizing aspects of Fauré’s harmony as extensions to the traditional RO model, as I do here.
15. Compare to Gjerdingen’s observation (2021, 70) about a harmonic-contrapuntal exercise by Fauré: “although his duo of bass and countermelody is completely diatonic, it forces subtle shifts in its perceived tonal orientation as it proceeds [due to a chain of parallel major thirds].”
16. This hierarchy is not unrelated to tonal hierarchies such as those described by Krumhansl (1990).
17. Cf. Tait (1989, 82–83), who relates this passage to Fauré’s letter to his son Philippe about the “Air de danse” from Caligula (Nectoux 1980, 258–259), which also involves ambiguity between G major and B minor. See also Gjerdingen’s comments on such tonal pairings (2021, 73 and 75).
18. I follow Richmond Browne’s (1981) term regarding the tonal implications of the diatonic set in his seminal article, though I use it here in the context of the RO. Since both the dom7 and the half-diminished are the rare seventh-chord subsets of the diatonic set, and since they are the only two sonorities containing the rare tritone, some of my present line of reasoning aligns with Browne’s logic. Moreover, one might say that the MM7 and mm7 seventh-chord subsets of the diatonic set are sonically and experientially similar to one another, whereas the tritone-containing dom7 and half-diminished subsets stand out and participate to a greater extent in position finding. Exploring the full implications of these parallelisms and qualifying them based on nineteenth-century usage lies beyond the present scope.
19. I am inspired here by Edward Klorman’s (2016) portrayal of the agency of different parts in chamber music.
20. As a reminder of functional discharges, see the tabulated summary in Harrison (1994, 92–93, figures 3.2–3.3).
21. As an anonymous reviewer of this article suggested, an additional explanation for this tricky $$^{4}_{2}$$ sonority is that it participates in parsimonious voice-leading above the bass layer in mm. 7–8: A–C$$\sharp$$–F to B$$\flat$$–D–F to B–D–F (or, one might add, perhaps A–C$$\sharp$$–F to A$$\flat$$–B$$\flat$$–D–F to G–B–D–F). This suggestion resonates with Cohn’s analysis of a passage from the Requiem, which I revisit below.
22. Again, my allusion here to subdominant chordal function shows my eclectic approach, despite my attempt to get maximal analytical mileage from the RO.
23. As Tait’s survey cited above suggests, the half-diminished in Fauré is often a dominant of V or, from the present viewpoint, bass $$\sharp\hat{4}$$.
24. As an example of such pedal points, see Nocturne No. 4 (Example 17a above), mm. 6–7. Compare also to the comments in Gjerdingen (2021, 70) about fauxbourdon in Fauré and as an improvised practice.
25. Compare also to the modal-mixture $$^{6}_{3}$$ substitutions on $$\hat{5}$$ in Examples 15a (m. 4) and 18a (m. 7).
26. There is, in fact, a strong sonic analog between Debussy’s instrumental “Clair de lune” and Fauré’s rendering of the words “au calme clair de lune triste et beau” in his setting of Verlaine’s poem (op. 46, no. 2): Fauré’s G$$\flat$$-major chord followed by A$$\flat$$ dom7 (mm. 38–41) have their counterparts in Debussy’s mm. 29–30 in the form of a D$$\flat$$-major triad followed by an E$$\flat$$ dom7.