When and How are Modulations Diatonic?

Yosef Goldenberg

Abstract

The common term “diatonic modulation” involves two distinct meanings: modulations into keys whose tonics are diatonic triads in the source keys (this study also distinguishes them from closely related keys) and modulations via a pivot chord that is diatonic in both source and target keys. Modulations may fulfill one condition but not the other. Modulations can reach a diatonic goal by several means: pivot chords that are chromatic in either the source key, the target key, or both; by means of enharmonic pivot chords; or without any pivot chords. Modulations can also reach some distant goals by means of pivot chords that are diatonic in both source and target keys. A corollary aspect of normative diatonic modulations is a stable phrase rhythm, but this can also be separated from diatonic modulations. The study also suggests pedagogical adaptation of the distinctions made, since they are missing in harmony textbooks.

View PDF

Keywords and phrases: Harmony, modulation, phrase structure, tonal music, key relations.

The subject of diatonic modulation is seemingly terra cognita, material of first-year undergraduate courses that can stimulate only pedagogical issues. Nevertheless, a renewed scrutiny discovers that the exact sense of how modulations are diatonic is complex and underexplored.

The term “diatonic modulation” is inexact, since diatonic music remains in one key,¹ while, by definition, a modulation moves from one key to another. This term thus certainly serves as a shorthand expression, but there are two distinct meanings according to which a modulation (or a brief tonicization) can count as diatonic.² One meaning is that the tonic of the target key is a diatonic triad in the source key (that is, in the major-minor system, the source key and target key are closely related). A different meaning is that there is at least one pivot chord, all the tones of which are diatonic members in both the source key and the target key.

This fundamental distinction is, surprisingly, missing from all major harmony textbooks.³ The absence of an explicit distinction between the different meanings of diatonic modulation probably owes to the large correlation between cases that obey both meanings or neither of them. Textbooks almost always initially present modulations that are diatonic in both senses, and to my knowledge all of them present diatonic modulations before introducing any chromatic chords other than secondary dominants, even in non-modulatory contexts. Edward Aldwell and Carl Schachter explicitly write (1989, 421) that the unit on diatonic modulations “concerns itself only with modulation to closely related keys” and that “other modulations will be reserved for later work in chromaticism.”⁴ This later work arrives in their very last chapter, and only shows modulations to distant keys with no pivot chords or with enharmonic pivots.⁵ Such an organization gives no place for non-enharmonic chromatic pivots in modulations to diatonic goals, nor to diatonic pivot chords to distant keys. The ways in which discussions of modulations are organized in other textbooks offer further problems: Robert Gauldin (2004) discusses most closely related keys (chapter 27, five chapters after the discussion of modulations into V in major or III in minor) before the chapter devoted to mixture chords (chapter 28), but in fact he briefly presents such mixtures already in chapter 26; both Miguel Roig-Francolí (2005, 478) and Stefan Kostka, Dorothy Payne, and Byron Almén (2013, 302) acknowledge “chromatic pivot chords” and “altered chords as common chords” before presenting modal mixture, but indeed what both books present are secondary dominants (see note 19 below). The gap in Aldwell and Schachter (1989) and confusions in other textbooks seem to arise from a theoretical muddle that deserves clarification, both for the goal of theoretical understanding and for the benefits of potential pedagogical improvements.

The present inquiry begins by elaborating on each of the two meanings of diatonic modulation. First, we observe modes other than major and minor, followed by pivot chords other than consonant triads. The remainder of the study examines modulations that fulfill one condition of diatonicism but not the other: 1. Modulations into closely related keys that have: (a) a chromatic pivot chord, (b) an enharmonic pivot chord, or (c) no pivot chord at all; 2. Modulations into distant keys by means of pivot chords that are diatonic in both keys.

1. Modulations to Keys Whose Tonic Functions as a Diatonic Triad in the Source Key: Beyond the Major-Minor System

Closely related keys are keys “whose key signatures differ by no more than one accidental” (Dunbar 2015, 399). Modulations into closely related keys count as diatonic because “the tonic of the new key functions as a diatonic chord in the old one” (Aldwell and Schachter 1989, 421).⁶ Even though, in the major-minor system, the group of closely related keys is identical with the set of keys whose tonics serve as diatonic scale degrees in the home key, the conditions are not identical.⁷ This becomes evident when one expands the system to include the other natural modes. Table 1 demonstrates how a major or minor triad can serve in key systems whose key signatures differ by one accidental in either direction.⁸

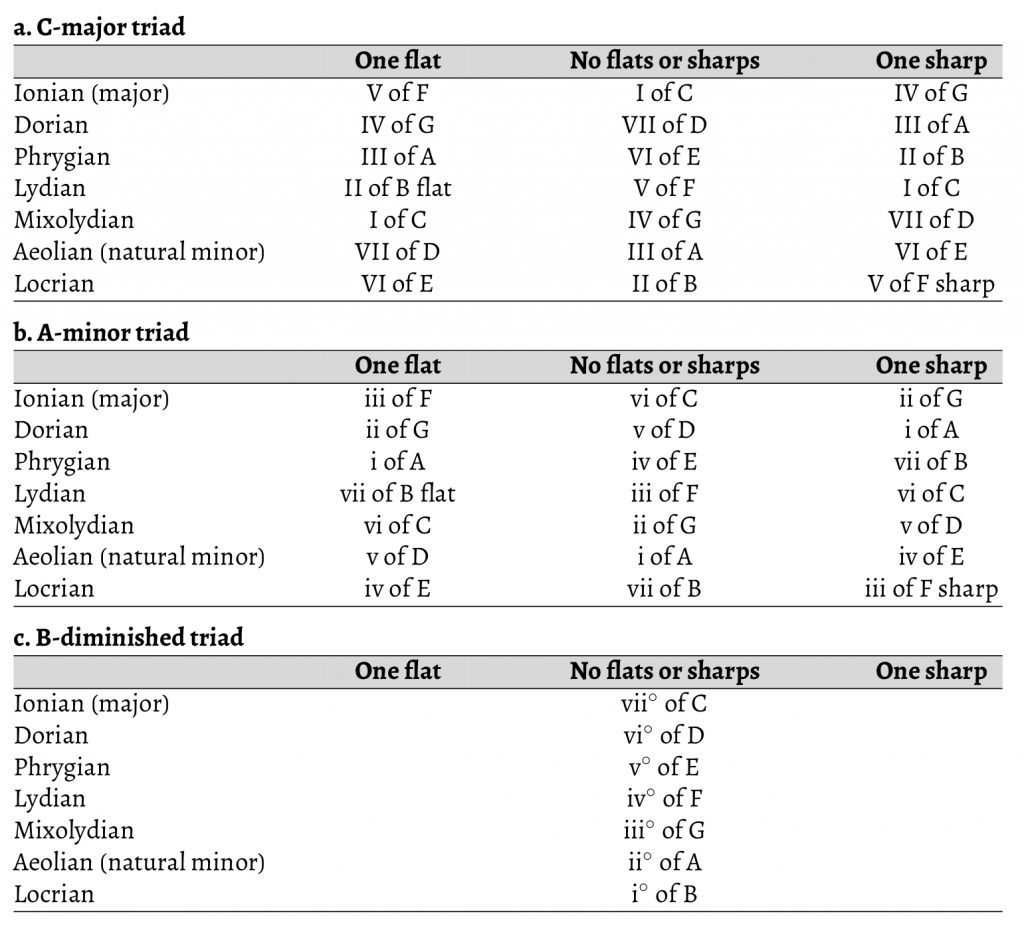
The major triad is also the tonic triad of a Lydian key system with one more sharp (or one less flat) or a Mixolydian key system with one more flat (or one less sharp), and the minor triad is also the tonic of a Dorian key system with one more sharp or a Phrygian key system with one more flat. All other modal diatonic scale degrees are also possible with one more sharp or one more flat in the key signature. By contrast, the diatonic diminished triad cannot function diatonically in keys with different key signatures, since it occurs only once in the diatonic set and thus both its root and fifth must be diatonic scale degrees (in C, both B$$\natural$$ and F$$\natural$$).

Modulating from major to Dorian on ii, Phrygian on iii, Lydian on IV, or Mixolydian on V cancels the difference in key signature. For example, modulating from C major to a key whose tonic is a D-minor triad (its ii) would normally add one flat to the key signature, but if the new tonic is in Dorian, there is no change in the key signature.

Dmitri Shostakovich’s Fugue in C major from op. 87 uses such modal modulations. This fugue has real entries (despite the salience of $$\hat5$$ early in the subject) on all diatonic tones. Since the subject lacks $$\hat7$$ and $$\hat2$$, there are only five (rather than seven) intervallically distinct forms of the subject in terms of exact semitones, as shown in Example 1. The second entry (first answer) is a real answer a fifth above, and since it has no form of F it could at first count as being in G major. In retrospect, after entries in the other diatonic modes, one understands the first answer as being in G Mixolydian.⁹

In Example 1, the expected change in accidentals is cancelled since the goal modes are flatter on the sharp side and vice versa. For example, the move to V (which normally entails an additional sharp in the key signature) is realized in Mixolydian (negating the expected additional sharp). An accidental should be added rather than cancelled when the goal mode is sharper on the sharp side or flatter on the flat side. Namely, modulations from a major tonic to Lydian (rather than to Mixolydian) whose tonic is the diatonic major triad on V or to Dorian (rather than to Phrygian) whose tonic is the diatonic minor triad on iii, require adding one more sharp (a difference of two accidentals in the key signature rather than only one in relation to the usual major V and minor iii). Similarly, modulations to Phrygian on ii or Mixolydian on IV would add one more flat (again, a difference of two accidentals in the key signature). In relative relations, it is likewise possible to introduce a change in key signature; one can even make a change of two accidentals in the key signature when one moves directly from tonic Dorian to relative Mixolydian (or vice versa). An actual case in point takes place in Marc Lavry’s 1940 Oratorio Song of Songs, excerpted in Example 2. The notated key signature of the passage has three sharps, but the passage actually begins in A mixolydian (two sharps only, G$$\natural$$ is indicated in the score) and moves to F$$\sharp$$ dorian (four sharps, D$$\sharp$$ is indicated in the score). This change of key system (in this case, not a fully established modulation) is quite abrupt, but that does not concern our current focus on the key relationships associated with our first meaning of diatonic modulation.

Example 3 abstracts the key relationships in the Lavry passage. The tonics of the two involved key systems are relative triads (F$$\sharp$$-minor and A-major triads, sharing the major third A–C$$\sharp$$), but the key signatures of these systems include two differences in accidentals (D$$\sharp$$ or D$$\natural$$, G$$\sharp$$ or G$$\natural$$). Thus, the basic notion that “relative keys share the same key signature” (Stone 2018, 21) is complicated outside the major-minor system.

2. Modulations by Means of a Pivot Chord that is Diatonic in Both Source and Target Keys: Beyond Consonant Triadic Pivot Chords

In strictly diatonic pivot chords, all the tones are members in both source key and target key. A pivot chord is necessarily placed on different scale degrees in each of the keys.¹⁰ In textbook demonstrations of pivot-chord modulations, the pivots are consonant triads (except in enharmonic modulations),¹¹ but diatonic pivots need not be consonant. The diminished triad can serve as a diatonic pivot chord between relative keys (ii^o becomes vii^o or vice versa). Even though it is difficult to avoid additional, consonant pivot chords, motivic relations can direct listening focus to the dissonant pivot. Example 4 shows a case in point.¹²

In Example 4, the ii of C minor sounds twice, once within the non-modulatory cadential progression, then after the cadence as the last chord before leaving the home key (moving to V/III, a member of C natural minor but not of C harmonic minor).¹³ The ii=vii of course occurs here as a seventh chord, a feature to be discussed shortly. The pivot is in $$4 \atop 3$$ inversion (two measures after its motivic preparation as $$6 \atop 5$$),¹⁴ and this $$4 \atop 3$$ proceeds as a subdominant (with $$\hat4$$ ascending to $$\hat5$$ in the bass).¹⁵

As we have just seen, diatonic pivot chords are not restricted to triads. Example 5a shows all possible diatonic pivot seventh chords.

Three seventh-chord types only take part in more than one key and thus have a potential to serve as diatonic pivots. If harmonic minor is assumed, the major-minor type appears only once, as V⁷ (in both major and harmonic minor), hence its apt name “dominant seventh chord,” and the diminished seventh chords can only serve (without enharmonicism) as vii^o7 in harmonic minor.¹⁶ The seventh chords with potential to serve as modulatory pivots are of the major-major and minor-minor types (each with four potential interpretations, two in major keys and two in minor keys; in natural minor the latter has one more potential location), and the half-diminished type (with two options). Interestingly, each of these three seventh chords has a different type of triad as its basis.¹⁷

Extrapolation into ninth chords preserves most of the identities in pivot chord qualities (see Example 5b). All four diatonic major-major seventh chords have diatonically the same ninth (an extra minor third, a major ninth above the root), three of the diatonic minor-minor seventh chords have another major third (preserving most of the potential of this pivot chord), and both diatonic half-diminished seventh chords remain diatonic in different keys with an added minor ninth (upper minor third).

I am not aware of actual diatonic pivot ninth chords in the literature, but pivot ninth chords are indeed possible, as the hypothetical composition in Example 6 shows (I⁹ = IV⁹). Notice that the ninth chord arrives as a genuine ninth chord (with its ninth as the dissonant member) but is left like an apparent ninth chord.¹⁸

3. Modulations to Closely Related Keys by Means of a Pivot Chord that is Chromatic in Either the Source Key, the Target Key, or Both

Pivot chords may be chromatic in the source key, the target key, or both. Roig-Francolí (2005, 597–602) aptly calls these, respectively, chromatic-diatonic, diatonic- chromatic, and chromatic-chromatic pivot relationships.¹⁹ The main context for Roig-Francolí’s discussion is modulation to distantly related keys, but one example in that chapter modulates to a close key—$$\flat$$II⁶ in F minor = IV⁶ in D$$\flat$$ major, a relatively widely-used pivot to be demonstrated below.²⁰

Among existing textbooks, Steven Laitz (2012) presents genuine chromatic pivot chords as well. Laitz asserts that “in a modulation to a chromatic key that results from modal mixture (such as $$\flat$$III or $$\flat$$VI), the pivot must be a mixture chord in the original key” (438). This assertion is not always true for keys two steps apart on the circle of fifths (see below). Laitz only presents chromatic pivot chords in the context of modulations to distant keys, and only in modulations that use mixture of the tonic itself and lend themselves to neo-Riemannian readings: from a major tonic, I goes via I$$\flat$$ to $$\flat$$VI in PL relations (for example, C–c–A$$\flat$$), or to $$\flat$$III in PR relations (for example, C–c–E$$\flat$$); from a minor tonic, I goes via I$$\sharp$$ to $$\sharp$$VI in PR relations (for example, c–C–a) or to $$\sharp$$III in PL relations (for example, c–C–e).

Later, Laitz presents the Neapolitan as a pivot chord (p. 467), and his paradigmatic example uses the $$\flat$$II as the pivot in a modulation into a closely related key as $$\flat$$II = IV. Example 7 adapts Laitz’s example. In the passage from Schubert’s Quartettsatz, the pivot chord is chromatic-diatonic, modulating from the C-minor tonic to its submediant.

Example 8, excerpted from Scott Joplin’s The Chrysanthemum, demonstrates the opposite direction, the diatonic-chromatic pivot IV = $$\flat$$II from a major key to its minor mediant.²¹ The phrase structure of Example 8 is very symmetrical. Excluding the final V that links back to the main key, this is a modulatory parallel period, whose antecedent ends with an imperfect authentic cadence. While often modulations fit loose phrase structures (Caplin 2010, 38), modulating periods are tight-knit. As in Schubert’s “Schäfers Klagelied” and the Quartettsatz above, the pivot chord first appears in the source key with no modulatory context. Within the modulatory parallel period, the moments when the chord appears (in the antecedent within a single key, in the consequent as a pivot) are analogous. This is a very common phenomenon in diatonic-diatonic modulations, and it reinforces both the symmetry of the period as a whole and the feeling of a well-prepared modulation.²² When the pivot is chromatic as in the Joplin excerpt, the symmetry helps to create something of a “diatonic aura” and thus serves as an independent determinant of diatonicism beyond the two precise meanings of diatonic modulation.

The opening of Johannes Brahms’s Intermezzo, op. 76, no. 4, given in Example 9, uses a chromatic-chromatic pivot chord: $$\flat$$VII of the main key becomes \flatII of vi.²³ The intermezzo opens on V⁷, which does not resolve for a long time, and the modulation to vi comes before any closed resolution in the tonic key (Salzer and Schachter 1969, 458–461). In this example, the pivot A\flat-major chord first sounds at the modulation itself, and thus one might be inclined to dismiss its function in the original key and regard it merely as a chromatic secondary subdominant.

Example 10 demonstrates a particularly clear use of a less common chromatic pivot, the minor IV in major, in Arthur Sullivan’s “There was a time” from the opera The Gondoliers. Like the Joplin example above, this is a tight-knit modulatory period of the kind usually associated with diatonic modulations. The triple hypermeter is a deviation from the norm, probably in this repertoire as well as in the Classical repertoire, but a symmetrical kind of deviation (Caplin 1998, 55). Nevertheless, the pivot chord is chromatic in the source key, and, in this example, the target key is remote. A chromatic chord similar (although not identical) to the pivot chord first serves in a non-modulatory antecedent, then the consequent uses a chromatic-diatonic pivot (iv [that is, IV$$\flat$$ = vi) to modulate to \flatVI.²⁴

In a systematic study of all possible chromatic pivot triads, each chord has a label in each key. Such a comprehensive account is given in Table 2. This table requires some explanations.

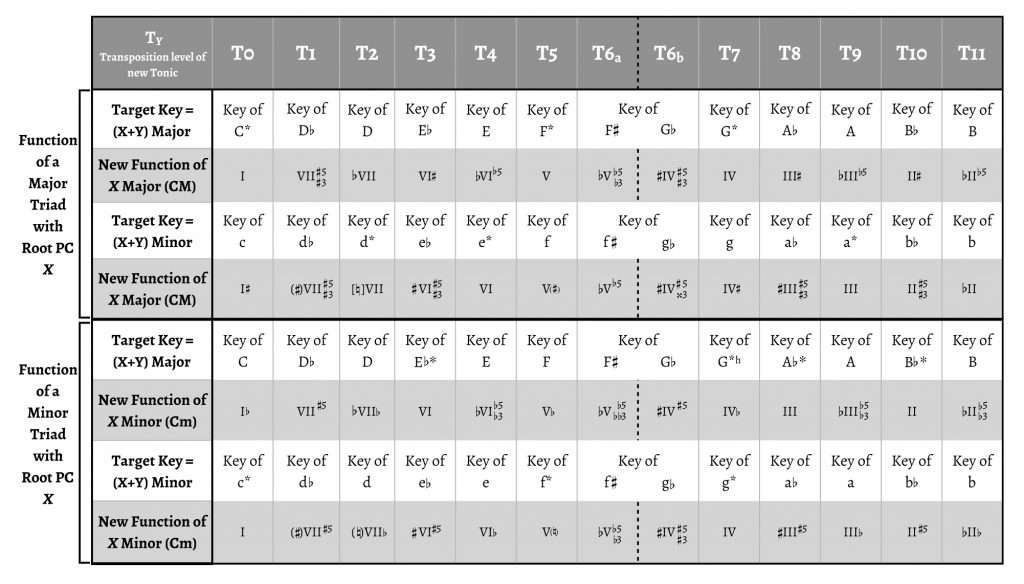
The table demonstrates C-major and C-minor triads in all major and minor keys and is generalizable under transposition to all consonant triads. For the sake of generalization, sharps and flats indicate respectively all raised and lowered tones, even when in the case demonstrated the altered tones would be naturals. For example, a C-minor chord in the key of E$$\flat$$ minor is $$\sharp$$VI^$$\sharp$$5, and both sharps indicate naturals (C$$\natural$$/E$$\flat$$ /G$$\natural$$) that are raised tones from the flats in the diatonic VI in E$$\flat$$ minor (C$$\flat$$/E$$\flat$$/G$$\flat$$).

The table indicates exactly all alterations from the diatonic versions of the scale degrees. For that purpose, accidentals to the left of the Roman numeral relate to the roots alone, and alterations of thirds and fifths are shown. Thus, the Neapolitan chord in major has also a lowered fifth along with the lowered root that it has in minor. Such lowered fifths (added to lowered roots) must not be confused with diminished fifths, which have no place in this table as it shows consonant triads alone. Alterations of the root alone or of the fifth alone only happen when the diatonic version of the triad is diminished. Elsewhere in this article, and especially in the examples, I retain the more usual nomenclature, where lowered roots indicate entirely lowered chords (e.g. $$\flat$$III for E$$\flat$$ major in relation to C major).

The indication of all alterations reveals certain cases that are not simply changes of mode, even when all alterations derive from modal mixture. Combinations of altered root and fifth create neo-Riemannian “slide” relations (major and minor triads with shared third).²⁵ What neo-Riemannian theory misses is the relations of these transformations to the diatonic grid, and as the table shows, the alterations can go both ways (e.g. a C-minor triad in A\flat minor is a raised slide from the diatonic III, C$$\flat$$ major, but a C-major triad in A major is a lowered slide of the diatonic III, C$$\sharp$$ minor).²⁶

In other cases, all chord members are altered. Most of these are disjunct mediants or submediants (Kopp 2002, 11). Two other entirely altered triads are the minor triads in major key T₁₁ (II with all tones lowered), and in minor key T₁ (VII with all tones raised). In the latter case, one of the raised tones is the leading tone, which is, of course, a basic alteration in harmonic minor. The most extreme situations involve, unsurprisingly, tritone relations. Two cases even give rise to double alterations of a single tone.²⁷ These are the only cases in which one might doubt the ability of the chords to serve as pivots.

In order to serve as a pivot, the triad will need to change its function from one key to another. Notice that the keys may be closely related even if the functions of the pivot are unconventional. As a partial reminder, the table marks with an asterisk those keys whose tonics are diatonic in C major and minor. But if the chord does not serve as tonic at all, then other keys may also participate in close relations. The alterations in pivots to closely related keys turn out to be always to the same side (e.g. C major as a pivot from A major to E major using lowered tones in both keys or from A$$\flat$$ major to E$$\flat$$ major using raised tones in both keys).

Readers may wonder whether modulations with such pivots really occur in the musical repertoire. In one sense, the complete view of potential pivots encompasses cases that are alternatively explained as a direct remote change of key. For example, Frank Lehman (2013, example 24) shows how VI$$\sharp$$, $$\flat$$VI, III$$\sharp$$, $$\flat$$III, VII$$\sharp$$, $$\sharp$$IV, and $$\sharp$$I (enharmonic equivalent of $$\flat$$II) of major keys can become new major tonics (I) by means of chromatically modulating cadential resolution. While Lehman’s examples arrive at the new tonics directly, other contexts may arrive at the same goals in a more gradual manner. Similarly, altered triads that can change into V in any key deserve special attention. Chords like II$$\sharp$$ or III$$\sharp$$ in major usually serve as applied dominants, but their modulatory pivot potential depends on an additional context in which they function in the main key only.²⁸ III$$\sharp$$ actually connects relative keys in cases when it locally implies the key of VI as an “apparent center,” but by the same time, takes part in a large-scale arpeggiation in the main key.²⁹

That said, for most of the potential chromatic pivots that arise in the complete systems shown in Table 2, I do not have examples from the literature. A possible hypothesis (which of course requires further research) is that many of these pivots are at work in repertories beyond common practice, such as the music of Francis Poulenc. Most probably, however, many options that the system includes remain hardly used. Such observations might point to a very specific manner of how the modernist narrative on the exhaustion of tonality must not be taken at face value: many options possible in the system were not in fact used.

Example 11, from Frédéric Chopin’s Rondo à la Mazur, op. 5, is our final instance of a chromatic pivot chord in the service of modulation into a closely related key. This excerpt demonstrates a dissonant chromatic-diatonic pivot. The target key is diatonic (III, a momentary goal that immediately progresses to V⁷), but the pivot is special.

Again, the phrase-structure of the modulation is tight-knit, as usually happens when a diatonic pivot is reinterpreted, but the pivot is not diatonic in the source key; it is a double chromatic alteration of the plagal II$$4\atop2$$, which serves as a common-tone chord. The altered II in the Rondo avoids its potential as VII/III and thus, a couple of measures later, becomes a true pivot in a modulation into III.

Within the target key III, the diminished seventh chord functions as diatonic vii^o$$4\atop2$$ (with the ordinary raised leading tone of harmonic minor). The following progression to V (of A minor) is complicated (but not overridden) by an interpolated augmented-sixth chord. Basically, it is a chromatic variant of the pivot chord II = VII that we encountered earlier in a diatonic form. Notice that the pivot chord, though both dissonant and chromatic, did not involve enharmonicism.³⁰

4. Modulations to Closely Related Keys by Means of Enharmonic Reinterpretation of a Pivot Chord

Enharmonic modulations usually serve an aesthetic effect of surprise³¹ by establishing remote key relationships.³² Nevertheless, close examination of all the options reveals that this need not be the case. Let us study each of the three common enharmonic pivots in turn:

a. Diminished seventh chords as enharmonic pivots are leading-tone seventh chords that connect keys whose tonics are a minor third apart. In a truly diatonic manner, all these tonics should be minor and thus remote from one another (three key signatures apart from each other), but in practice, diminished seventh chords nevertheless often resolve into a major tonic. This enables enharmonic modulations to connect close, relative keys.³³

In Example 12, the enharmonic reinterpretation takes place in the service of a brief tonicization of the relative major. The aesthetic effect is so distant from any striking character usually ascribed to enharmonic reinterpretations and specifically to those based on the diminished seventh,³⁴ that the enharmonicism is hardly noticeable at all.

The same pivot takes place in Example 13, this time on the way back from an implied VI (G$$\sharp$$ minor) to the tonic (B major). The VI is implied by the previous III$$\sharp$$, where neighboring chords guarantee that the sense of V/VI is at work. Chopin notates the diminished seventh chord accordingly, first with F𝄪, as if going to G$$\sharp$$ minor, but then the chord changes its inversion enharmonically and resolves to the tonic of the section, B major.

A case of enharmonic modulation to the relative minor (back from the relative major to the main tonic) takes place in the first ending of Franz Joseph Haydn’s String Quartet, op. 20, no. 5 (not shown). This is the first example that Kostka, Payne, and Almén (2013, 297) use to demonstrate enharmonic modulation based on a reinterpretation of a diminished seventh chord. Dissonant leaps in the upper voice indeed highlight this chord, but the entire context is extremely stable: a link from the goal of the exposition back to the minor tonic. The authors’ designation of the enharmonic pivot as vii^o7 (of A$$\flat$$ major) = vii^o$$6\atop5$$ (of F minor) does not indicate that in the former (major) key, the chord is altered, while in the latter (harmonic minor) key, it is the expected form of vii7 (diatonic with raised leading tone).

b. The augmented triad has no diatonic function (since III in minor usually uses the natural form). Enharmonic interpretation of augmented triads by means of a single semitonal displacement in both directions (as shown in Cohn 2000, 93) connects pairs of relative triads (potentially relative keys). For example, C/E/G$$\sharp$$ as [III]^$$\sharp$$5 of A minor is enharmonically equivalent to C/E/A$$\flat$$ as [VI]^$$\flat$$6 of C major.³⁵ Other potential tonics of closely related keys can be achieved through a single semitonal displacement in one direction, and a double displacement in the other direction (C/E/G$$\sharp$$ as V^$$\sharp$$5 of F major in relation to C/E/A$$\flat$$ in C major, or C/E/A$$\flat$$ as IV^$$\flat$$6 in E minor equivalent to C/E/G$$\sharp$$ in A minor)

c. The enharmonic pivot involving V⁷ and the German augmented-sixth chord does not lend itself easily to modulations into closely related keys.³⁶ The German chord in its normal location as an altered IV leads eventually to a tonic (major or minor) whose root lies a semitone below the resolution of its enharmonic counterpart V⁷. However, if the V⁷ is applied to IV in major, then the minor triad one semitone below is diatonic in the original key (V⁷/IV is enharmonically equivalent to German$$\sharp6\atop5$$ of III). David Beach and Ryan McClelland (2012, 130–132) have shown this route skillfully in Ludwig van Beethoven’s Horn Sonata (not shown) as one of several paradigmatic enharmonic modulations. What they do not call attention to is that the target key of that enharmonic modulation is closely related to the source key.³⁷

5. Modulations to Closely Related Keys Without a Pivot Chord

Modulations without pivot chords are undertheorized. Some modulations that usually count as having no pivot chord do not really avoid a pivot: in modulations by common tone, the last chord of the source key and the first chord of the target key usually serve as stable tonics without a connecting process, but they may be regarded as pivots one of whose functions is I. In modulations by sequence, the last chord of each statement could be labeled in the next statement. Some textbooks do not cover true modulatory processes without pivot chords.³⁸ I refer to situations where the last chord in the old key is unstable (not a tonic), and it is followed by an unstable chord in the new key. Aldwell and Schachter (1989, 555–556) present modulations by chromatic inflection, which partly cover the pro- posed type of pivotless modulations.³⁹ While this procedure may connect distant keys,⁴⁰ it may also work in modulations to closely related keys. For example, the transition of Beethoven’s “Appassionata” sonata—shown in Example 14—modulates to the expected relative major key, but it uses none of the multiple potential pivot chords. Rather, the last chord in the tonic is the V, using the lead- ing tone, precisely the one tone that distinguishes the tonic harmonic minor from the target key. The next chord is a widely stretched V⁷ of III, using the diatonic $$\hat7$$. A short anticipation gives rise to a momentary incomplete diminished seventh chord that should not count as a genuine pivot. There is a certain case, however, for interpreting E$$\natural$$ enharmonically as F$$\flat$$, since the descending minor second F$$\flat$$–E$$\flat$$ brings in the target key the motivic $$\hat6$$–$$\hat5$$ semitone, which serves as the motto of the work as a whole. That the $$\hat6$$ is minor (a product of mixture in A$$\flat$$ major) both anticipates the closing group in A$$\flat$$ minor and reinforces the motivic connection to the D$$\flat$$–C in the main key.⁴¹

Sometimes the old and new dominants do not occur in immediate succession but are instead linked by a modulatory process. Yitzhak Sadai (1980, 466) shows a strongly convincing case in point from Chopin (Example 15), modulating from VI (in major) back to the overall tonic. The process includes V/V but is mostly non-functional. It uses several techniques in succession: 1. three chromatic variants of A in mm. 49–51 (A$$\flat$$, A$$\natural$$, A$$\sharp$$); 2. a single succession of semi- tonal contrary motion between the outer voices in m. 51;⁴² and 3. expected resolution in the bass to B in m. 52 while the other parts avoid the expected B-major chord.⁴³

Finally, the unstable chords at the boundary point between the old and new keys need not be dominants. In the abstract harmonic progression in Example 16 (after Wagner [1980, 49]), the first chord in the goal key is the French augmented-sixth chord (altered II$$4\atop3$$).⁴⁴ The chord before it is V/V of the source key, not strictly diatonic but able to lead to a V–I non-modulatory closure. That progression remains entirely functional.

6. Modulations to Keys with a Difference of Two Accidentals in the Key Signatures by Means of a Pivot Chord that is Diatonic in Both Source and Target Keys

It is possible for modulations to reach keys with a difference of two accidentals in their key signatures by means of pivot chords that are strictly diatonic in both source and target keys. Already, Johann Philipp Kirnberger ([1771–1779] 1982, 123, discussed in Damschroder [2008, 210]) presents these options, although he thinks of the pivots as intermediate keys. Arnold Schoenberg ([1911] 1978, 272–273) develops these ideas into a systematic discussion. Example 17 realizes in musical notation the pivots Schoenberg finds. Example 17a demonstrates pivot chords from major keys to keys two steps apart around the circle of fifths, whereas 17b does the same for a minor source key.⁴⁵ Later textbooks do not present this discussion coherently: Walter Piston distorts it,⁴⁶ while current harmony textbooks avoid the subject altogether or make imprecise statements.⁴⁷ Schoenberg’s discussion is valuable not only in that it is not too narrow (as in textbooks that limit diatonic pivots to modulations between closely related keys) but also in that it is not too wide (including only pivots that are truly diatonic).⁴⁸

Strictly diatonic pivot triads are impossible for keys that are more distantly related than those discussed above. Omitting potential pivots that are diatonic in natural minor only, there remain four optional pivots (all of which can of course work in both directions): ii (of a major key) = iii (of a major key); iii (of a major key) = iv (of a minor key); IV (of a major key) = V (of a major or, by extension, harmonic minor key); V (of a major or, by extension, harmonic minor key) = VI (of a minor key).

The V = VI pivot takes place in an intricate way in the slow movement of Brahms’s second cello sonata (Example 18). Graham Hunt (2009, 103) summarizes the tonal structure of the three-key exposition as I–$$\flat$$i–V. The first two keys are F$$\sharp$$ major and F minor, with a change in the notated key signature from six sharps to four flats. In fact, the first key can be spelled as G$$\flat$$ major, and the second key is vii[^$$\sharp$$5] (minor VII, while the diatonic form is diminished). These keys are two steps apart on the circle of fifths, and the means of the modulation is a diatonic pivot chord V = VI (C$$\sharp$$/D$$\flat$$ major). The music never cadences strongly on F, and eventually reverts to D$$\flat$$. The motion toward F minor is real, however. The example notates the original key as its flat equivalent in order to make it easier to follow the modulation.⁴⁹

The V of harmonic minor as a diatonic chord in an ex- tended view of the minor system serves as a kind of joker that can function as a pivot chord between very remote keys. Example 19 demonstrates this device in the much- discussed opening of Schubert’s “Auf dem Flusse” from Winterreise, D. 911, no. 7:⁵⁰ V of E harmonic minor = VI of D$$\sharp$$ minor. (The example offers two variants of understanding the harmony in the goal key). The goal key has two sharps more than E major, the parallel key of the source key E minor, and five more sharps than the actual source key.

The progression I (or i)–V = VI–V–i is not far removed from modulations without pivot chords such as those encountered above: V in one key is followed by V in another key. Nevertheless, the smoothness of that particular progression does depend on the membership of the source key’s V in the target key.⁵¹

Examples of the other potential diatonic pivots between remote keys are rare, especially between two major keys a whole tone apart.⁵² Schoenberg ([1911] 1978, 272–74) provides abstract cases. Example 20 reproduces progression (a) from Schoenberg’s Example 208, with Roman numerals added. Schoenberg notices the V = IV pivot, which he also tonicizes by an applied leading-tone seventh chord. As he similarly tonicizes the pivots in all six progressions of his example, he apparently conceives of them as intermediate tonics. The next chord, iii⁷ = ii⁷, is an additional pivot, but Schoenberg does not refer to it.⁵³

Example 21 brings an actual example of the same pivot chord from Beethoven, now in the opposite direction, as IV = V. This example is a modulation back to the key of B$$\flat$$—the main key of the secondary theme group—after a detour to C, by means of IV = V.⁵⁴

The following examples show the iii = ii pivot. Example 22 shows three abstract examples by Schoenberg, Max Reger, and Paul Hindemith, respectively. Schoenberg again tonicizes the pivot chord; Reger’s example, from his treatise on modulation, is extremely condensed, as are all the examples in the treatise. Sometimes they suggest a formalization of modulatory plans that may be carried out more slowly, albeit Reger was often as abrupt in his compositions (see Example 24 below). Hindemith actually uses the V = IV pivot as well (as did Schoenberg in Example 20), and the iii = ii begins a new subphrase and seems to serve as the main pivot.⁵⁵

Example 23 presents an actual example by Muzio Clementi modulating to the flat side. Clementi’s passage opens the development section on A major and modulates to G major via the pivot ii = iii (B minor), which is briefly tonicized by means of a secondary dominant (similar to Schoenberg’s practice in his abstract demonstration). The progression in this example is schematic and straightforward, but its aesthetic impact is not entirely convincing.⁵⁶ It is quite astonishing that such exceptional modulations as those in Examples 21 and 23 (Beethoven and Clementi, respectively) come from normative works of common-practice tonality. At least the Beethoven passage sounds smooth to the extent that its exceptional modulation is hardly noticed.

7. “Non-diatonic Phrase Structure” of Strictly Diatonic Modulation

In several examples (notably Examples 7 [Schubert], 8 [Joplin], and 10 [Sullivan]), we have encountered modulations that involve chromatic elements but have a tight-knit phrase structure that helps to create an impression of stability usually associated with diatonic music. The opposite is also true: modulations that are diatonic in both senses, i.e., move into a diatonic key by means of a diatonic-diatonic pivot chord, nevertheless may have a haphazard phrase structure that gives the aesthetic effect (what I deem “energies”) of an abrupt modulation. The Reger excerpt in Example 24 implies, for a moment, the key of the diatonic II before going further to the diatonic III. The motion from F major to the (unrealized) G minor is performed by means of a pivot chord that is diatonic in both keys (B$$\flat$$ major, IV = III). Unlike the minor form iv = iii, which connects remote keys, the IV = III connects closely related keys. Nevertheless, the aesthetic effect is so striking that one might be surprised to learn that the modulation is, after all, diatonic in both senses.⁵⁷

Examples like the Reger excerpt indicate that the classification and analysis of specific modulatory passages must include aspects of phrase structure along with the relations of keys and identities of pivots.

Epilogue

The basic harmonic concept “diatonic modulation” concerns two distinct facets in its strict meaning, and an additional aspect of phrase structure. Directing our attention to areas where the various aspects do not coincide helps to sharpen our understanding of what diatonic modulation is within the material that lies at the center of first- year harmony courses and beyond.

The current state of knowledge lacks a database of actual examples of all modulations. Such a database should include all possible relations between source keys and target keys, all meanings of pivot chords (in both directions) when they exist, and details of modulatory process when no pivot chords exist. Only a database that would cover repertories in their entirety would enable truly empirical knowl- edge of modulations, their frequency, and their distribution in the repertoire.

For further clarification of concepts of diatonic modulations, I strongly endorse an extensive study of repertories such as film music, folk music (at least from Europe, where relations to Western tonality are direct), and twentieth-century post-Romantic and neo-Classical extended tonality. The present study has already included a glimpse beyond the tonal common practice in order to show that diatonic relations between keys involve two distinct conditions (difference of no more than one accidental between key signatures and membership of the new tonic in the old key).

While the main purpose of this study is theoretical, some of its insights deserve pedagogical adaptation. Much of the material it covers slips between the cracks: basic courses in harmony leave out most of the situations raised here due to their complexity or rarity, but advanced courses in music analysis hardly ever fill gaps in the knowledge of harmony. Instead, they tend to go on to analytical application and advanced methods such as Schenkerian or neo-Riemannian theories.

Certainly, a course for beginners should not enter into all the details proposed here. However, when presenting diatonic modulations for the first time, it is advisable to explicitly state both senses in which the modulation is diatonic. At that stage, it is unnecessary to engage situations that fulfill one condition but not the other, and if students raise the question, the distinctions can be delayed until more advanced lessons. Instructors who hold a clear picture of the entire palette of potential modulations are likely to better offer clear and efficient explanations. Advanced classes and theory majors should be exposed also to less common types of modulations.

The presentation in harmony textbooks of some kinds of modulations, notably of pivotless modulations, is incomplete and often poor. This indicates theoretical lacunae that lie beyond pedagogical compromises. A theoretical lesson is that the nuts and bolts of music theory turn out to be fields that still offer areas for future research. This is true of musical form—a field in which our understand- ing has deepened so much in recent decades—and, also, of harmony and counterpoint.

---

Yosef Goldenberg teaches at the Jerusalem Academy of Music and Dance, where he also serves as head librarian. He is a theorist of tonal music and scholar of Israeli music. He is the author of Prolongation of Seventh Chords in Tonal Music (Edwin Mellen Press, 2008) and co-editor of Bach to Brahms: Essays on Musical Design and Structure (University of Rochester Press 2015), winner of the Society for Music Theory’s 2016 Outstanding Multi-Author Publication Award. On music theory, he has published in Indiana Theory Review, Journal of Music Theory, Journal of Schenkerian Studies, Music Analysis, Music Theory and Analysis, Music Theory Online, and Theory and Practice. Currently, Yosef Goldenberg works on a full-length study of enharmonicism.

References

Agmon, Eytan. 1995. “Functional Harmony Revisited: A Prototype-Theoretic Approach.” Music Theory Spectrum 17 (2): 196–214.

———. 1996. “Conventional Harmonic Wisdom and the Scope of Schenkerian Theory: A Reply to John Rothgeb.” Music Theory Online 2 (3). http://www.mtosmt.org/issues/mto.96.2.3/mto.96.2.3.agmon.html.

Aldwell, Edward, and Carl Schachter. 1989. Harmony and Voice Leading, 2nd ed. New York: Harcourt Brace Jovanovich.

Beach, David. 1983. “A Recurring Pattern in Mozart’s Music.”Journal of Music Theory 27 (1): 1–29.

Beach, David, and Ryan McClelland. 2012. Analysis of 18th- and 19th-Century Musical Works in the Classical Tradition. New York: Routledge.

Brown, Matthew, Douglas Dempster, and Dave Headlam. 1997. “The $$\sharp$$IV($$\flat$$V) Hypothesis: Testing the Limits of Schenker’s Theory of Tonality.” Music Theory Spectrum 19 (2): 155–183.

Caplin, William E. 1998. Classical Form: A Theory of Formal Functions for the Instrumental Music of Haydn, Mozart, and Beethoven. Oxford: Oxford University Press.

———. 2010. “What Are Formal Functions?” In Musical Form, Forms & Formenlehre: Three Methodological Reflections, edited by Pieter Bergé, 21–40. Leuven: Leuven University Press.

Capuzzo, Guy. 2004. “Neo-Riemannian Theory and the Analysis of Pop-Rock Music.” Music Theory Spectrum 26 (2): 177–199.

Christ, William, Richard DeLone, Vernon Kliewer, Lewis Rowell, and William Thomson. 1966. Materials and Structure of Music, I. Englewood Cliffs, N.J.: Prentice-Hall.

Clendinning, Jane Piper, and Elizabeth West Marvin. 2005. The Musician’s Guide to Theory and Analysis. New York: W. W. Norton.

Cohn, Richard. 2000. “Weitzmann’s Regions, My Cycles, and Douthett’s Dancing Cubes.” Music Theory Spectrum 22 (1): 89–103.

Damschroder, David. 2006. “Schubert, Chromaticism, and the Ascending 5–6 Sequence.” Journal of Music Theory 50 (2): 253–276.

———. 2008. Thinking About Harmony: Historical Perspectives on Analysis. Cambridge: Cambridge University Press.

Dunbar, Brain. 2015. Practical Music Theory: A Guide to Music as Art, Language, and Life. U.S.A.: Factum Musicae.

Gauldin, Robert. 2004. Harmonic Practice in Tonal Music, 2nd ed. New York: W. W. Norton.

Harrison, Daniel. 1995. “Supplement to the Theory of Augmented-Sixth Chords.” Music Theory Spectrum 17 (2): 170–195.

Hindemith, Paul. (1943/44) 1968. A Concentrated Course in Traditional Harmony, Book I, Revised ed. New York: Schott.

Horwood, Frederick J. 1948. The Basis of Harmony. Toronto: Thompson.

Hunt, Graham. 2009. “The Three-Key Trimodular Block and its Classical Precedents: Sonata Expositions of Schubert and Brahms.” Intégral 23: 65–119.

Kirnberger, Johann Philipp. (1771–1779) 1982. The Art of Strict Musical Composition. Translated by David W. Beach and Jürgen Thym. New Haven: Yale University Press.

Kopp, David. 2002. Chromatic Transformations in Nineteenth-Century Music. Cambridge: Cambridge University Press.

Kostka, Stefan, Dorothy Payne, and Byron Almén. 2013. Tonal Harmony, 7th ed. New York: McGraw-Hill.

Laitz, Steven G. 2012. The Complete Musician: An Integrated Approach to Tonal Theory, Analysis, and Listening, 3rd ed. New York: Oxford University Press.

Lehman, Frank. 2013. “Hollywood Cadences: Music and the Structure of Cinematic Expectation.” Music Theory Online 19 (4). http://www.mtosmt.org/issues/mto.13.19.4/mto.13.19.4.lehman.html.

Lewin, David. 1982. “Auf dem Flusse: Image and Background in a Schubert Song.” 19th-Century Music 6 (1): 47–59.

———. 1987. Generalized Musical Intervals and Transformations. New Haven: Yale University Press.

Marlowe, Sarah Rose. 2013. “Fugue in Context: A Schenkerian Approach to Select Works by J. S. Bach and Dmitri Shostakovich.” PhD diss., University of Rochester.

McCreless, Patrick. 1996. “An Evolutionary Perspective on Nineteenth-Century Semitonal Relations.” In The Second Practice of Nineteenth-Century Tonality, edited by William Kinderman and Harald Krebs, 87–113. Lincoln: University of Nebraska Press.

Morris, Robert. 1998. “Voice-Leading Spaces.” Music Theory Spectrum 20 (2): 175–208.

Nobile, Drew F. 2011. “Form and Voice Leading in Early Beatles Songs.” Music Theory Online 17 (3). http://www.mtosmt.org/issues/mto.11.17.3/mto.11.17.3.nobile.html.

Ottman, Robert W. 1998. Elementary Harmony: Theory and Practice, 5th ed. Englewood Cliffs, N.J.: Prentice-Hall.

———. 2000. Advanced Harmony: Theory and Practice, 5th ed. Englewood Cliffs, N.J.: Prentice-Hall.

Piston, Walter. 1948. Harmony, 2nd ed. New York: W. W. Norton.

Pomeroy, Boyd. 2011. “The Major Dominant in Minor-Mode Sonata Forms: Compositional Challenges, Complications, and Effects.” Journal of Schenkerian Studies 5: 59–103.

Reger, Max. (1903) 19uu/2013. On the Theory of Modulation. Translated by John Bernhoff. New York: Dover.

Riemann, Hugo. 1887. Systematische Modulationslehre. Hamburg: Richter.

Roig-Francolí, Miguel A. 2005. Harmony in Context, 2nd ed. New York: McGraw-Hill.

Rothgeb, John. 1996. “Re: Eytan Agmon on Functional Theory.” Music Theory Online 2 (1). http://www.mtosmt.org/issues/mto.96.2.1/mto.96.2.1.rothgeb.html.

Rothstein, William. 1991. “On Implied Tones.” Music Analysis 10 (3): 289–328.

Sadai, Yitzhak. 1980. Harmony in its Systemic and Phenomenological Aspects. Jerusalem: Yanetz.

Salzer, Felix, and Carl Schachter. 1969. Counterpoint in Composition: The Study of Voice Leading. New York: McGraw-Hill.

Schachter, Carl. 1987. “Analysis by Key: Another Look at Modulation.” Music Theory Spectrum 6 (3): 289–318.

Schenker, Heinrich. (1906) 1954. Harmony. Edited by Oswald Jonas and translated by Elisabeth Mann Borgese. Chicago: University of Chicago. Abridged translation.

———. (1935) 1979. Free Composition, Translated and edited by Ernst Oster. New York: Longman.

Schoenberg, Arnold. (1911) 1978. Theory of Harmony, Translated by Roy E. Carter. London: Faber & Faber.

Schwanzara, Ernst, ed. 1950. Anton Bruckner: Vorlesungen über Harmonielehre und Kontrapunkt an der Universität Wien. Vienna: Österreichischer Bundesverlag.

Smith, Peter H. 1997. “Brahms and Motivic 6/3 Chords.” Music Analysis 16 (2): 175–217.

Stone, Stephen C. 2018. Music Composition and Theory: A Practical Approach. New York: Rowman and Littlefield.

Tymoczko, Dmitri. 2011. A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice. Oxford: Oxford University Press.

van Egmond, René, and David Butler. 1997. “Diatonic Connotations of Pitch-Class Sets.” Music Perception 15 (1): 1–29.

Wagner, Naphtali. 1980. Assignments in Harmony (Targilim Be-Harmonia). Jerusalem: Academon.

Yellin, Victor Fell. 1998. The Omnibus Idea. Detroit: Harmonic Park Press.

1. In a general sense, diatonicism does not dictate monotonality and could embrace pieces that change their tonal center (See Example 1 below). In Tymoczko’s (2011, 6) terms, the diatonic set serves as a macroharmony even without centricity. However, in tonal music, passages that modulate to the relative key would not count as diatonic.
2. The difference between true modulation and brief tonicization is essential in other respects but does not matter for our purposes. Examples that occur on the surface level (such as Example 12 below) give rise to the same kind of observations that come up in cases that concern more salient modulations.
3. Some textbooks do address the diatonic quality of pivot chords as a separate issue. See below.
4. All of Aldwell’s and Schachter’s observations on modulations are already present in the second edition (1989) and remain unchanged in later editions. In addition to textbooks discussed specifically in this paper, I have also examined Ottman (1998 and 2000) and Clendinning and Marvin (2005).
5. The example of modulation by chromatic sequence (Mozart, Requiem K. 626, Confutatis; Aldwell and Schachter 1989, 559) eventually ends in a closely related key, but only after intermediate distant local keys.
6. Aldwell and Schachter place this statement in a definition of closely related keys, within their chapter on diatonic modulation.
7. As is common knowledge, these keys are ii, iii, IV, V, and vi in major and III, iv, v, VI, and VII in natural minor, but (minor) v and (major) VII are not available in harmonic minor. By way of extension, accepting the major V as a diatonic member in harmonic minor opens the way to a modulation into a distant key (four steps around the circle of fifths). Although minor v remains the more frequent variant of the dominant as a goal in a large-scale tonal plan, the major V does serve as a goal in certain works in minor (Pomeroy 2011). Pyotr Ilyich Tchaikovsky’s Piano Trio, op. 50, I, even includes a remote change in key signature (from no sharps in A minor to four sharps in E major), which merely indicates a move to the harmonic-minor V.
8. The table includes the Locrian mode for the sake of completeness. As is well known, its dissonant “tonic” triad makes its usage problematic.
9. For a discussion of the diatonic modes in this fugue, see Marlowe 2013, which also summarizes a Russian-language discussion by Alexander Dolzhansky and Lev Mazel.
10. Without that condition, change to the parallel mode by means of the V that is shared between major and harmonic minor would count as modulation.
11. See Aldwell and Schachter 1989, 420–426; Gauldin 2004, 386–401; Roig-Francolí 2005, 468–476. Steven Laitz (2012, 380) does show, in the abstract only, vii^o6 = ii^o6 among the pivot chords from I to vi. Kostka, Payne, and Almén (2013, 299) use that pivot in an abstract assignment.
12. Franz Schubert composed precisely the same progression in “Ständchen” (Schwanengesang no. 4). Compare m. 6 (ii^ø$$6 \atop 5$$ within a closed progression in minor) to m. 12 (the same chord becomes vii^ø$$6 \atop 5$$ in the tonicization of the relative major).
13. Throughout this paper, I refer to harmonic minor as possibly diatonic by way of extension (along with the natural minor). René van Egmond and David Butler (1997, 2) trace that idea back to Hugo Riemann and find that the argument “has the attractive feature that the leading tone is considered an intrinsic part of the set, rather than a chromatic tone.”
14. For motivic usage of single chords, see Smith 1997.
15. For the potential of vii to serve as a subdominant chord, see Agmon 1995, 201 and 210.
16. In major, vii^o7 is not at all possible diatonically, although this is the usual form of applied vii^ø7 to the major triad V in minor keys. See for example Schubert, Impromptu, op. 90, no. 1, m. 19. Strictly, had the members of the applied leading-tone chord been diatonic in the key of the major V, a major form of the seventh ($$\hat6$$ in the momentary key, $$\hat3$$ in the overall key) should have been used, but in fact the overall diatonic minor form of $$\hat3$$ is in use.
17. For pivot seventh chords, see VI$$4 \atop 2$$ of C-sharp minor = IV$$4 \atop 2$$ of its III, E major, in J. S. Bach, Prelude in C-sharp minor from the Well-Tempered Clavier, vol. 1, m. 5, as analyzed by David Beach and Ryan McClelland (2012, 53). As the authors note (p. 357, n. 2.9), “having the pivot occur on a seventh chord is relatively rare.”
18. Apparent ninth chords are analogous to apparent seventh chords, “complexes of tones that appear to be seventh chords but that in fact are not, since the dissonance is not caused by a 7th above the root” (Aldwell and Schachter 1989, 390).
19. Roig-Francolí’s application of these terms in his book is problematic, as most of his examples for chromatic pivot chords are not genuine pivot chords at all, but rather present a secondary V in the home key as a primary V in the secondary key (pp. 478–480), or a secondary V in another key (p. 603). Frederick Horwood (1948, 96) already suggests the categories laid out by Roig-Francolí, but unusually incorporates diatonic-chromatic and chromatic-diatonic pivots under diatonic modulation: “diatonic modulation occurs when the pivot chord is diatonic in both keys, or in either of them.”
20. Roig-Francolí’s example 26.4 (2005, 601) comes from Johannes Brahms’s Sonata for Clarinet and Piano, op. 120, no. 1, I, pivot at m. 33.
21. For another example of the pivot that turns IV into $$\flat$$II, see Robert Schumann “Widmung,” op. 25, no. 1. The B section in $$\flat$$IV, which becomes $$\flat$$II of the main key.
22. See for example Tchaikovsky, Waltz from Album for the Young, mm. 1–16. As in the Joplin example, the consequent modulates to III after an antecedent that ends with an imperfect authentic cadence. The opening tonic becomes in the consequent a pivot chord (VI of III). A related symmetry also takes place when a phrase that is closed in the tonic includes a chord that becomes a pivot in an ensuing modulatory phrase. See Schubert, Impromptu op. 90, no. 1: a closed module in mm. 34–37 with salient VI in m. 34 is followed by a modulatory repeat where VI ultimately becomes the local tonic of a new key.
23. The initial move to $$\flat$$VII is smoothed out through reinterpretation of the preceding common-tone diminished seventh harmony.
24. Another example of IV$$\flat$$ in the source key as a chromatic-diatonic pivot: Schubert, Symphony No. 4, IV, mm. 143–147. IV$$\flat$$ of C$$\flat$$ becomes III of its $$\flat$$II (C; enharmonic spelling notwithstanding). This is the foreground carrier of the tonicization of the immediate step within a chromatic passage. For the context, see McCreless 1996, 92–93. This passage is close to a chromatic 5–6 sequence (Damschroder 2006), but an entirely contrapuntal explanation is misleading, since the intermediate minor chord is in root position without an actual B/C$$\flat$$ in the bass (actually, it is realized as a dyad without the fifth at all), and since the IV$$\flat$$ = III is followed by a strong V in the next momentary key.
25. The term “slide” comes from Lewin 1987, 178. Robert Morris (1998, 187) shows the same relations on a Riemannian grid as P’. Guy Capuzzo (2004, 178) has already noted their equivalence.
26. The slide relations between minor chords on VI (in major or minor) and major chords on V involve enharmonic relations ($$\flat\hat6$$ ∼ $$\hat7$$), as happens in the fate motive from Richard Wagner’s Der Ring des Nibelungen. This situation can bring enharmonic notations of minor VI as a $$\hat5$$ in $$\sharp$$II. See Tchaikovsky, Symphony No. 5, I, m. 23. A similar problem occurs with a minor chord in a major key at T₁₁.
27. Tritone key relations are problematic from any approach. Matthew Brown, Douglas Dempster, and Dave Headlam (1997, 160–161) discuss their conflict with the Schenkerian Ursatz and also their absence in Arnold Schoenberg’s chart of regions and their “unconnected” status in Donald Tovey’s table of key relationships.
28. For III$$\sharp$$ that avoids the context of V/VI, see Frédéric Chopin, Polonaise Militaire, op. 40, no. 1, m. 5. II$$\sharp$$ that avoids the context of V/V is unlikely in common-practice tonal music, but exists in popular music, as in the Beatles’s song “Eight Days a Week” (Nobile 2011, Example 10).
29. See the development sections of Mozart’s Piano Sonatas K. 280 and K. 332. Beach (1983) shows V–III$$\sharp$$–I as the large-scale structure of these development sections. In both, however, the III$$\sharp$$ sounds locally as V/VI. For structural chords that are local dominants implying tonics that do not participate in the large-scale structure, see Schachter 1987, 295–98. Schachter’s term “apparent centre” is interchangeable with what William Rothstein (1991, 314–17) calls “implied keys.” See also Example 13 below.
30. Another example of a common-tone chord as a pivot chord: Schubert, Symphony No. 9, IV, m. 119 and m. 137. The former phrase uses vii^o$$4\atop3$$ of A minor (II in G major), while the corresponding identical chord in the latter phrase becomes a common-tone chord resolving to D major (V of G major). Unlike the example from Chopin’s rondo, the Schubert excerpt does involve enharmonic reinterpretation of the diminished seventh chord.
31. See for example Schenker [1906] 1954, 333: “The effect of modulation by an enharmonic change is . . . drastic and surprising.”
32. Some textbooks present enharmonic modulations only within chapters explicitly devoted to modulation to foreign keys. See Gauldin 2004, 719–726; Roig-Francolí 2005, 605–614.
33. The voice leading from the vii^o7 in Example 12 is unusual. In the same movement, compare mm. 195–199 and m. 201. Other examples: 1) Schubert, Symphony No. 4, IV. Compare the diatonic vii^o7 in C harmonic minor at m. 13 with its enharmonic transformation into vii^o$$4\atop2$$ with a lowered seventh (in the bass) at the modulation into the relative major (m. 29); 2) Felix Mendelssohn, Elijah, No. 1 (“Hilf, Herr!”). The movement begins in an immediate progression from D minor to the relative F major: I–vii^o7 = vii^o$$4\atop2$$/III–V⁷/III–III.
34. Aldwell and Schachter (1989, 561) cite Anton Bruckner: “the diminished seventh [is] like the Orient Express: it could take you rapidly to the most distant places.” The original may be found in Schwanzara 1950, 281. I am thankful to Eric Lai and Nicolas Meeùs for locating this.
35. Instead of the designation of the literal III and VI, one might indicate I^{$$\sharp$$5–6} and I^{$$\flat$$6–5} respectively. See debate on this issue in Rothgeb 1996 and Agmon 1996.
36. The same is true for the other augmented-sixth chords and their enharmonic equivalents: V$$7\atop\flat5$$–French pair or incomplete V$$7\atop3$$–Italian.
37. Beethoven, Horn Sonata, op. 17, I, mm. 134–150. Another exam- ple: Chopin, Etude, op. 10, no. 7, mm. 7–9. Rare types of augmented- sixth chords can give rise to further enharmonic modulations to closely related keys. For example, the “Tristan” chord and the “Till” chord, two different equivalents of the half-diminished seventh chord, can lead to relative keys (the “Tristan” spelling {F, G$$\sharp$$, B, D$$\sharp$$} is in A minor; the “Till” spelling [transposed] {F, A$$\flat$$, B, D$$\sharp$$} directly resolves to C major). Daniel Harrison (1995, 185) discusses the similarity (but hardly the difference) between these chords.
38. Gauldin 2004; Kostka, Payne, and Almén 2013; Laitz 2012 (despite misleading clues in his index [871] in subcategories of “tonicization of modulation”); Roig-Francolí 2005. Gauldin (2004, 712), however, includes a related passage from Wagner’s Siegfried, in which the internal organization is no less daring, but eventually does not modulate at all.
39. The example Aldwell and Schachter bring from Beethoven’s Piano Sonata, op. 106, stems from the stable tonic that becomes III$$\sharp$$.
40. See Schubert, Impromptu, op. 90, no. 2, mm. 251–258 (in the coda). In that passage, there is no inflection, but the succession I–V in B minor followed by V–I in E$$\flat$$ minor supports an octatonic tetrachord in the melody.
41. Another example, in service of a modulation a third down (from III to I in major), is found in the example that Aldwell and Schachter (1989, 508, reference from p. 556) bring from Schubert, Symphony no. 9, I, mm. 24–29: I–V in E minor followed by V⁷–I in C major. The change between the old and new dominants is a case of chromatic inflection.
42. More complete usage of the chromatic wedge often gives rise to the omnibus progression. However, in Victor Fell Yellin’s (1998) comprehensive study of the omnibus, there is not a single example that modulates between two stable key areas.
43. Another, simpler, example of a link between a back-relating V of the old key and a V of a new key: Haydn, Mass no. 11, “Nelson,” I, mm. 36–40. V of the opening D minor moves by unaccompanied chromatic passing motion to V of F.
44. The origin of Example 16 is a mostly unrealized figured-bass assignment. It uses the German form of the augmented-sixth and ends in G major.
45. Schoenberg deals earlier (ibid., 207–221) with modulations to more remote keys, a discussion in which he suggests shortcuts by means of modal mixture.
46. Piston (1948, 84) attempts to find pivot chords for C and B$$\flat$$. Although by B$$\flat$$ he means B$$\flat$$ major, for C he uses all the forms found in either C major or C minor.
47. See Kostka, Payne, and Almén 2013, 291: “Whereas any pair of closely related keys will have at least one diatonic triad in common, this is not always the case with foreign key relationships” (my emphasis).
48. Unlike Schoenberg, Max Reger ([1903] 19uu/2013) considers various pivots, not necessarily diatonic in the strict sense (diatonic-diatonic pivots). This choice lets him find a richer spectrum of modulations, but it obscures the special group of modulations by diatonic-diatonic pivots alone.
49. On a more local level, the motion from D$$\flat$$ moves via an augmented-sixth chord (beat 2 of m. 18) that serves as a potential V⁷/IV within a local modulation a third up, as in the enharmonic modulation in Beethoven’s horn sonata mentioned above. The readings are compatible on different structural levels.
    Another example of V = VI that directly leads to a cadence: Tchaikovsky, Romeo and Juliet, introduction, m. 21: V of F$$\sharp$$ [G$$\flat$$] minor becomes VI of F minor; then in sequence V of F minor (m. 51) becomes VI of E minor.
50. See Schenker [1935] 1979, Fig. 40, No. 2; Lewin 1982. The observation I present here is my own.
51. The opposite direction, VI of a minor key = V, is the diatonic basis of a pivot that exists in the introduction to Beethoven’s Symphony No. 4, I, mm. 22–23 as $$\flat$$VI of a major key = V (with added seventh) of $$\flat$$II (that never resolves properly). Laitz (2012, 590–592) uses this excerpt for an analytical interlude.
52. Along with V = VI, iii = iv also connects a major key and a minor key whose tonic is one semitone lower. These relations are familiar from enharmonic modulations by means of V⁷–German$$6\atop5$$ pivot chords.
53. Progression (b) in Schoenberg’s Example 208 is shown below as Example 22a. As to the rest of the same example, progressions (c), (d), and (f) start from A minor and use the natural $$\hat7$$; progression (e) moves from C major to B minor via iii = iv (Schoenberg’s indication of G major as an additional intermediate key is incorrect). Progression (a) in Schoenberg’s example 209 moves from C major to B$$\flat$$ major using IV = V and ii = iii respectively.
54. The earlier modulation from B$$\flat$$ to C (mm. 79–80) is enharmonic: vii^o7 of VI {F$$\sharp$$, A, C, E$$\flat$$} becomes vii^o$$6\atop5$$ before a cadential $$6\atop4$$ in C major {F$$\sharp$$, A, C, D$$\sharp$$}. Spelling according to the structural goal (vii^o7/V) would miss the enharmonic change and fail to explain the startling experience of that moment.
    For IV = V, see also the large-scale construction of the opening of Schubert, Moment Musical no. 2. The first section in F minor ends on its IV (B$$\flat$$ minor), which becomes a harmonic-minor V of the next section in E$$\flat$$ minor (spelled D$$\sharp$$ minor). Another example of IV = V: Schubert, Symphony no. 9, III, m. 17, demonstrated in Christ et al. 1966, 464–465.
55. Riemann (1887) also systematically presents modulations into various targets, but he intentionally avoids modulations into keys in whole-tone relations. I am indebted to Alexander Rehding for that reference.
56. The example opens the development section of the movement. After the exposition ends in the dominant key, the structural role of the tonic in the opening of the development is not clear. Please note that Example 23 comes from a sonata, not from the sonatina with the same opus number.
57. As an alternative, one might wish to read the E$$\flat$$-major chord in m. 3 as a chromatic-diatonic pivot ($$\flat$$VII of F major = VI of G minor). Nevertheless, that chord functions as a secondary subdominant. Had the IV into which it resolves continued into a cadence in the source key, we would have a single-key phrase.