Proto-Harmony and the Problem of Tonal Centricity in Rachmaninoff’s All-Night Vigil

Ellen Bakulina

Abstract

This article explores the Russian concept of proto-harmony (pra-garmoniia) from both a theoretical and an analytical angle. Proto-harmony was introduced by Andrei Miasoedov (1998) as a group of four diatonically related triads that does not require an overarching tonal center, and that (according to him) serves as the tonal basis of much Russian music. In the first, theoretical section, I offer my own approach to proto-harmony that allows for greater theoretical and analytical precision and that engages in a dialogue with other, non-Russian approaches such as Neo-Riemannian and set theories. I introduce the notion of the proto-harmonic complex (PH complex) and show that it belongs to a family of similar diatonic groups explored by Western scholars, including “component keys,” “Axis progression,” “double-agent complex,” and paired relative keys (or Russian “mutability”). In the second, analytical section, I show that, in movements 1 and 14 from Sergei Rachmaninoff’s All-Night Vigil (1915), a proto-harmonic complex explains large-scale non-monotonal structures by controlling important formal boundaries. Proto-harmony thus interacts with the decentralization of entire pieces that defy a conventional tonal explanation in either harmonic-functional or Schenkerian terms.

View PDF

Keywords and phrases: Rachmaninoff, tonality, harmony, Russian music theory.

Russian church music abounds with hymns that begin and end on different harmonies and thus challenge traditional Western concepts of tonality. Let me begin with two examples (Example 1), borrowed from a collection of Russian glas hymns (glasovye pesnopeniia).¹ Of course, with some effort, one could wedge these hymns into conventional tonal concepts, but there are problems at every step. If the first piece (Example 1a) is “in F major,” why does it neither begin nor end on the tonic? If it is “in G minor,” why does it modulate at the end? If the second hymn (Example 1b) is “in C major,” again, why does it avoid the tonic chord at the formal extremes, especially at the final cadence, which is arguably deceptive? If it is “in A minor,” why does it avoid either authentic or plagal progressions in that key? Or is each of these pieces in two different keys, thus exemplifying tonal pairing?

Attempted tonal explanations from the viewpoint of Western major-minor tonality leave the impression that these hymns are somehow loosened or incomplete (given that they do not reach the tonic by the end), or perhaps disunified, if one prefers a dual-key view. Or perhaps one could simply say that these hymns are not exactly tonal. But if this is true, then what replaces tonality in them? In fact, Russian-language scholarship offers a theoretical tool that answers this question without resorting to any ideas of incompleteness or duality. This tool is proto-harmony (translated from the Russian pra-garmoniia), introduced by the present-day Russian theorist Andrei Miasoedov in his 1998 treatise Garmoniia russkoi muzyki (Harmony of Russian Music), a treatise that remains untranslated from the original Russian.² Miasoedov explains proto-harmony as a diatonic group of four triads, which does not demand a unity of tonal center. The two hymns in Example 1 exemplify such chordal groups: C–D(d)–F–g in the first and G–a–C–d in the second. (The chromatic element in the first hymn, F$$\sharp$$, will be explained later.)

Proto-harmony, therefore, represents one of the concepts that effectively deals with problems posed by non-monotonal music. In English-language theory, since the publication of The Second Practice of Nineteenth-Century Tonality (1996), edited by William Kinderman and Harald Krebs, a whole trend of writings about non-monotonality has appeared. Alternatives to monotonality have been explored in Romantic repertoire, rock music, jazz, Russian church music, Baroque instrumental works, and Italian opera.³

Ideas related to non-monotonality are important in Miasoedov’s treatise, but, in my view, this and other aspects of his work can be greatly developed. Although he insists, at the beginning of his book, that proto-harmony does not require a single center, he never explores the effect that this idea has on events beyond brief chord-to-chord progressions. This seems to be a significant shortcoming, given that the idea of centricity concerns levels as big as entire pieces. Miasoedov’s theory provides rich soil for further theorizing and for a more elaborate analytical apparatus.

Therefore, taking inspiration from Miasoedov’s theory, I develop my own approach that allows for greater theoretical and analytical precision, is better adapted for the analysis of large non-monotonal structures, and engages in a dialogue with other, non-Russian theories. In the first, theoretical section of this article, I begin by offering modifications to basic concepts associated with proto-harmony, by introducing the term PH complex and letter notation for proto-harmonic chords. Then, using terminological apparatuses well-known to English-language theorists, I show that the proto-harmonic group belongs to a family of similar diatonic groups, which I call harmonic complexes, all of which entail, in one way or another, attenuated or shifting tonal centers. Along the way, I clarify the distinction between proto-harmony’s conceptual diatonic basis, its original scalar context, and chromatic elements that it can acquire in specific musical contexts.

In the second part of the article, I apply the concept of the PH complex to the analysis of large-scale musical structures: two complete movements from Sergei Rachmaninoff’s All-Night Vigil, op. 37. In both movements, proto-harmony interacts with large-scale form, producing a tonal structure decentered from a traditional Western viewpoint. I show how a PH complex “unfolds” over an entire piece by controlling important formal boundaries. Viewing this music in proto-harmonic terms allows one to see its internal structural unity, which is not apparent from the methodological perspectives of harmonic-functional and Schenkerian theories.⁴ In addition, I show the structural relationship between the Vigil and Russian church music in general, which may not be easily recognized by non-Russian musicians. The latter goal is important, as many are familiar with Rachmaninoff’s piano and orchestral music exclusively; this limited perspective overlooks the origins of the kinds of structures we find in the Vigil.

In a sense, my objective is to connect proto-harmony with as many other analytical methods as possible. This connection is important because the concept is unknown to non-Russian scholars and thus needs contextualization. Just as important, however, is that Miasoedov’s writing engages other theories only minimally; when it does, he tends to contrast his own method to those of others, rather than enter a dialogue that would reveal methodological or conceptual connections.⁵ Part of this attitude results from his wish to “discover” only those harmonic aspects that make Russian music uniquely Russian; any ideas that, in his view, fail to perform this job, are dismissed as either irrelevant or mistaken.⁶ The present article aims to illuminate theoretical concepts that can enrich our understanding of proto-harmony, and that show just those musical elements that remain unexplained without a proto-harmonic view.

1. Miasoedov’s Theory of Proto-Harmony: A Summary

Let me start with some background. The concept of proto-harmony is the theoretical and analytical focus of Miasoedov’s 1998 treatise, which surveys Russian music from supposedly pre-historic times up to Prokofiev. Miasoedov’s central thesis is that proto-harmony forms the structural basis and is a defining national feature of much of Russian music, as opposed to Western tonality defined by its tonic-dominant opposition, its standard syntax, and its modulatory processes.⁷ The subtitle of the book is, tellingly, “the roots of nationally specific features” (korni natsional’noi spetsifiki).⁸ Important, and relevant to my ensuing analyses, is the predominance of church music in his examples: Miasoedov insists that Russian proto-harmonic structures originate from ancient folk and liturgical contexts, specially stressing the important of liturgical music throughout his book.

To explain proto-harmony as a purely diatonic phenomenon would misrepresent its workings in many specific musical situations, as we will see shortly. Nonetheless, the diatonic basis is important for proto-harmony’s historical formation (at least, according to Miasoedov’s own explanation). Example 2 offers a summary of this formation. The example begins with the idea that, in the ancient times, Eastern-Slavic folk and church music used a diatonic collection of four notes, which can be ordered by perfect fifths (a), or else presented as two major seconds separated by a minor third.⁹ Later, these tones became the bottom notes of perfect fifths (c), and then the roots of diatonically related triads (e). Given an abstract C-major scale (and not necessarily the key of C major), these triads are scale degrees I, ii, vi, and V, consistently labeled with upper-case Roman numerals throughout his treatise.¹⁰

Miasoedov never states that a piece that contains elements of proto-harmony must employ only the chords of a proto-harmonic group. Such an exclusive use of proto-harmony occurred, according to him, only in ancient times. In the music of the nineteenth and twentieth centuries, proto-harmony coexists with tonality. This coexistence means that one might find passages or textural layers which exclusively use proto-harmonic chords, or encounter specific individual harmonies being emphasized in clearly tonal contexts, such as ii in major and iv in minor. Two aspects characterize proto-harmonic passages in Miasoedov’s book. First, he often singles out excerpts that violate the rules of standard tonal syntax. Second, he insists on the equality of status (ravnopravie) among the chords of proto-harmony. “Among the four given triads,” he says, “any one of them may take the role of ‘tonic’” (1998, 19).¹¹ When tonality and proto-harmony coexist, proto-harmony imbues tonal structures with a degree of decentralization, an “independence from an overarching center” (21). This idea is kindred to another Russian concept, mutability (peremennost’), a modal/tonal organization characterized by the coexistence or rivalry of multiple centers, usually diatonically related. In the context of major-minor tonality, mutability is conceptually similar to tonal pairing; Yuri Kholopov specifically dubs it tonal mutability, in contrast to modal mutability. The most well-known type of tonal mutability is the relative-mutable mode (parallel’no peremennyi lad), which refers to the pairing of relative keys. I will return to this concept in the discussion of the harmonic complex.¹²

Here is a working definition of proto-harmony, based on Miasoedov’s theory and formulated for the purposes of further theoretical discussion. Proto-harmony refers to a diatonic (at least at its structural basis) group of four triads, two major and two minor, characterized by the following elements: (1) the triadic roots can be ordered by perfect fifths; (2) the syntactical rules are relaxed, compared to classical tonality; and (3) the unity of system as a foundation of musical cohesion overrides the unity of tonic. The group is diatonic at least at its structural basis, if not always on the musical surface.

2. Structural Properties of Proto-Harmony: The PH Complex

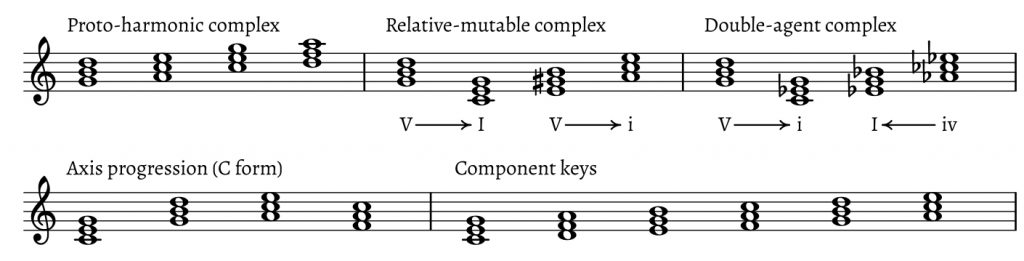
In this section, putting Miasoedov’s writings temporarily aside, I further develop the idea of proto-harmony by offering sharper conceptual distinctions, contextualizing it with respect to non-Russian theories, and exploring the structural properties of the proto-harmonic group, particularly its internal symmetry and structural balance. I also suggest the notion of the harmonic complex, to refer to chordal groups (of which proto-harmony is one) characterized by decentralization. A comparison of these chordal groups, including the “Axis progression” of pop music, paired relative keys, and Carl Dahlhaus’s “component keys,” among others, suggests an explanation for chromatic variants of proto-harmonic members.

As a first step, let me adopt the concept of proto-harmonic complex, or PH complex. While proto-harmony refers to chord relationships as a general idea, a PH complex is an instantiation of this idea at a specific pitch level, just like a key is a specific instantiation of the idea of tonality. In the equal-temperament universe, there are twelve PH complexes. A triad that participates in a PH complex may be called a PH member. Let me further distinguish between a complete and a partial PH complex. A complete PH complex consists of four triads, such as those in Example 2, which can be transposed to any pitch level. A partial PH complex omits any one of the four members.¹³ As a second step, I introduce letter notation for the PH complex, as shown in my initial examples; lower-case letters stand for minor triads. The principle is borrowed from popular music studies, specifically the recent work of Scott Murphy (2014) and Mark Richards (2017). Richards uses letter notation for what he terms the “Axis progression,” the chordal group a–F–C–G, which could be transposed to any pitch level and start with any chord, to rotate through the other three. Like the PH complex, the Axis progression is fundamentally diatonic and often involves an unclear tonal center, or mutability, as Russian theorists would say, hence the potentially misleading role of Roman numerals, which are necessarily tied to a single tonic. In a PH complex, depending on context, letters may replace or supplement Roman numerals, which may still be necessary if a specific situation suggests a tonal (or dual-tonal) understanding.¹⁴

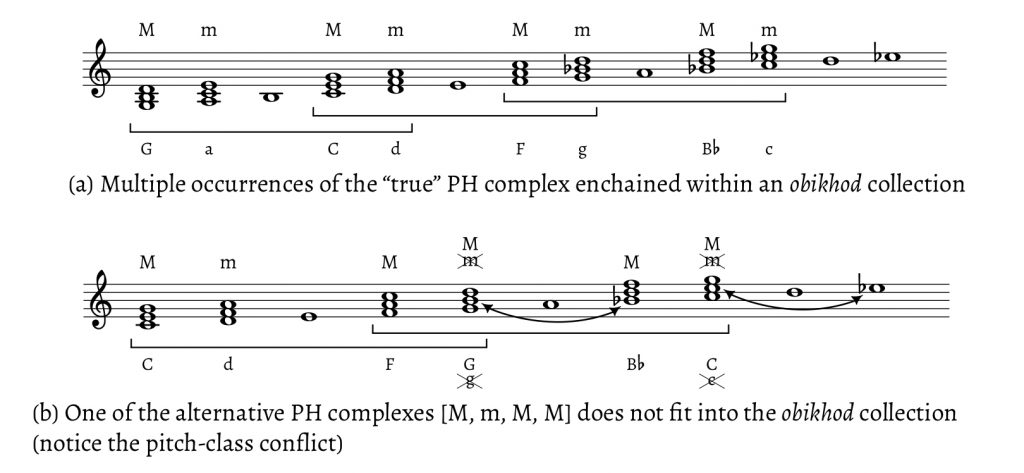
Some important differences notwithstanding, this approximate analogue to the PH complex in contemporary Anglophone popular music suggests an exploration of proto-harmony in broader terms with respect to other potentially similar chordal groups. I begin this exploration by describing the PH complex in set-theoretical terms, which provide the most systematic tools for a comparison of proto-harmony with other like structures. The four triadic roots of a PH complex form the set class 4–23[0257], a subset of other familiar structures that are segments of the circle of fifths: 5–35[02479]—the pentatonic scale, 6–32[024579]—the Guidonian hexachord, and 7–35[013568T]—the diatonic scale. Discussions of diatonic structures in set-theoretical terms have precedents. Robert Gauldin (1983) has explored the properties and possible origins of certain diatonic structures, with an emphasis on pentatonic and heptatonic (7-note) scales.¹⁵ All scales coordinated by perfect fifths are termed the cycle-7 complex, defined as any set “generated by successive applications of the multiplier ic 7” (41).¹⁶ Gauldin offers two tables, reproduced in my Example 3, that include sets of all cardinalities that fit into the cycle-7 category. The first table (“PC AXIS SYSTEM”) includes, among other things, the pentatonic, the heptatonic (7-note diatonic scale), and the 3–1[027] set class (which Miasoedov proposes as the oldest, 3-note form of the 4-note proto-harmony). The second table (“IC AXIS SYSTEM”) includes the proto-harmonic tetrachord 4–23[0257], the Guidonian hexachord 6–32[024579], and an eight-note scale crucially important for Old Russian church music, called the obikhod collection (obikhodnyi zvukoriad, 8–23[0123578T]).¹⁷

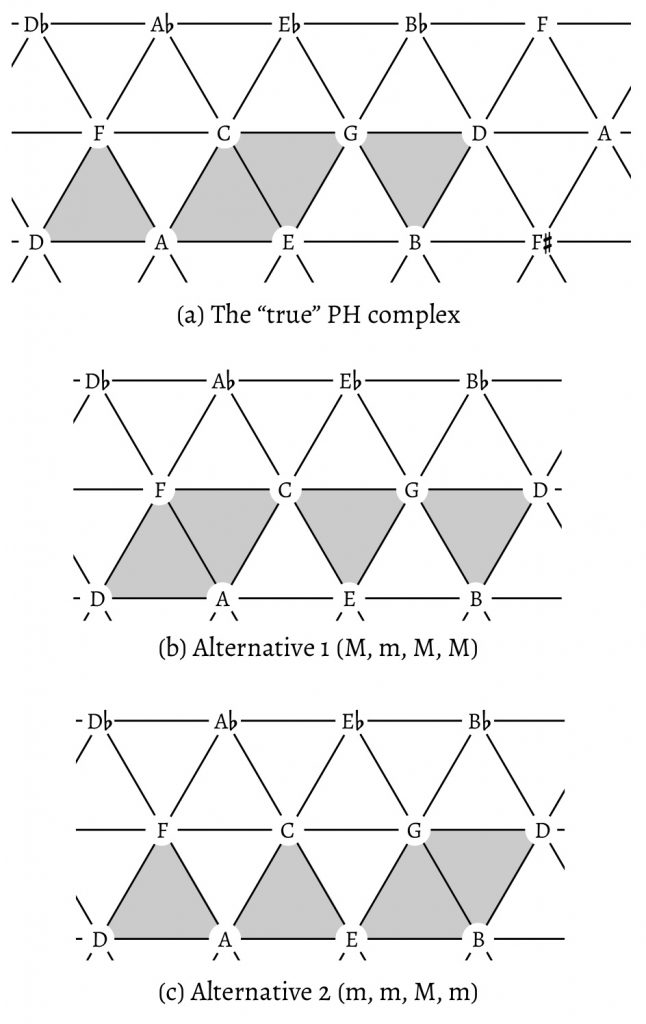
The obikhod collection briefly brings us back to Miasoedov and his scalar derivation of proto-harmony. This is important for reasons both theoretical and historical since, according to Miasoedov, proto-harmony formed in an era that preceded modern tonality and the supremacy of the heptatonic diatonic. The main theoretical issue here is the coordination of two basic criteria of proto-harmony: root relationships (by fifths) and triad quality (two major, two minor). To put the matters in set-theoretical terms, the chordal roots of any complete PH complex form a 4– 23[0257] set, but not every [0257] set produces a true PH complex. For example, the triads with roots G–A–C–D, a representative of the [0257] set class, forms a PH complex in the context of the natural system (i.e., the C-major scale), but not in the systems shifted one fifth higher or lower on the circle of fifths (the one-flat and one-sharp scales). What would proto-harmony look like if it was defined only by the first criterion—i.e., only fifth relationships, and not the consonant triad qualities—in the context of, say, the seven-note diatonic scale? Such a definition would result in two more possibilities with respect to chord quality, which I suggest calling the hypothetical proto-harmonic alternatives. Example 4 shows these alternatives, one with three major triads (MmMM, in this case C–d–F–G) and the other with three minor (mmMm, in this case d–e–G–a). The reader will notice that the first “alternative” contains, in a different order, the chords of Richards’s Axis progression.

The reason why these two alternatives fail to satisfy Miasoedov’s proto-harmonic theory lies in the original scalar context of proto-harmony. Prior to the adoption of (evolving) functional tonality, imported to Russia from the West around the turn of the eighteenth century, the structural basis of Russian music was not the 7-note, but the 8-note obikhod collection, found on line 4 on the IC axis system of Gauldin’s table. Example 5 details the relationship of the obikhod collection to the PH complex, symmetrically related both as scales and as stacks of fifths. The obikhod collection includes both B$$\natural$$ and B$$\flat$$ and involves a recurrence of the pattern [whole tone, whole tone, semitone] at the perfect fourth. In relation to the obikhod collection, the PH complex is what Gauldin, following Joseph Yasser, refers to as an “infra-diatonic system,” a smaller number of structurally prior tones within a larger diatonic collection.¹⁸ Conversely, the obikhod collection functions with respect to the PH members as “limited macroharmony,” Dmitri Tymoczko’s term for a scale as compositional basis, rather than as a tool for measurement. Example 6 shows why the obikhod collection allows for only one of the three triad groups of Example 4—that is, why the hypothetical alternatives don’t work. Each of the alternatives would require chromatic inflections that compromise the integrity of the collection.¹⁹ As one compares the “true” proto-harmonic group with the alternative groups, one feature immediately stands out: the internal symmetry and balance of the true PH complex. This balance is due to (1) the equal number of major and minor triads, (2) their strict alternation, if the roots are put in the normal form {0,2,5,7}, and (3) their balanced relationships, mapped on a Neo-Riemannian Tonnetz in Example 7. The more balanced structure of the true PH complex is apparent here by virtue of its symmetrical shape (Example 7a), compared to the two more skewed alternatives (Examples 7b and 7c). This symmetry is significant if one compares the PH complex with other important chord groups such as the three tonal functions Tonic–Subdominant–Dominant, which form a symmetrical structure (the subdominant and dominant are a fifth below and above the tonic, respectively).

Moreover, the symmetry of the true PH complex bears implications with respect to the major-minor tonal system, implications that have to do with the position of the R-related pair as potential tonics—the pair with two common tones. In the true PH complex, this pair is in the center. Each one of these two chords is flanked by a fifth-related “companion”—C major’s major dominant and A minor’s minor subdominant. In each of the alternatives, however, the R-related pair is on the side instead of the center, and one of its members does not get a companion function, thus preventing the complex from interacting comfortably with major-minor tonality. In the MmMM group, the minor member of the relative pair, the D-minor triad, has a major S, the G chord, and this suggests a Dorian mode incompatible with strictly Classical tonality. In the mmMm group, the major member of the relative pair, the G chord, gets a minor dominant. The problematic fifth-related pair G–d is the same in both cases.

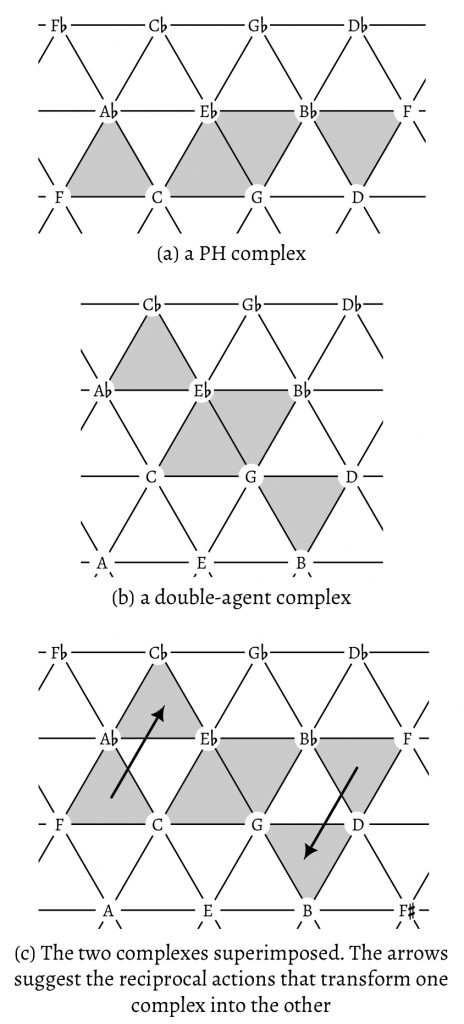
Interestingly, the PH complex as presented in Example 8 has many parallels with a similar chord group often used in Western Romantic music, a group Richard Cohn (2012, 72–76) has termed the “double-agent complex,” here G–a$$\flat$$–c–e$$\flat$$. Example 8c juxtaposes the two complexes and demonstrates their close relationship: in both, two R-related triads are in the center, and each of these triads has a fifth-related companion. Unlike in the PH complex, in the double-agent complex the major chord is flanked by its minor subdominant, rather than major dominant, and the minor chord is flanked by its major dominant, rather than its minor dominant. Significantly, Cohn suggests that any member of the double-agent complex can function as a temporary tonic: the complex is “tonally adaptable” (Cohn 2012, 74).

The relevance of proto-harmony to several other chord groups I have cited so far suggests a generalization. It would be naïve to suppose that proto-harmony, the Axis progression, the relative-mutable mode, and the double-agent complex are all built upon the same principle and differ only with respect to their chordal components. And yet, they share enough to suggest the idea of a harmonic complex, in which more than one chordal member can assume the role of a center—that is, be elevated to the highest level of tonal hierarchy.²⁰ One may call this a certain “hierarchical flexibility” within a harmonic complex. This hierarchical flexibility does not necessarily endanger the overall centricity within a work (although this often is the case). Rather, it means that, within the complex, more than one member has the potential to exert tonal control, in the presence of the other members, in a whole piece or a section.

Example 9 shows the complexes discussed so far side by side, adding one more—Dahlhaus’s “component keys,” to be discussed shortly. Differences among the complexes include (1) chord order, which is strictly fixed only in the Axis progression but free in the others; (2) the potential of the group members to be separated by other events, that is, to serve as middleground harmonies (once again, Axis is an exception, since, by Richards’s definition, it is strictly a chord-to-chord progression);²¹ and (3) hierarchy within the group—that is, the number of harmonic members that can serve as a temporary or global tonic. This last point is the most complicated and requires a longer discussion. But I will mention that the relative-mutable complex can have only two harmonies as tonics; the two dominants are always subordinate to them. The Axis progression also allows for a maximum of two centers (C major and A Aeolian), but the other two harmonies have a more flexible functional relationship to these tonics: for instance, G may be a lower neighbor of A minor or upper fifth of C major; C may or may not be subordinated to a; etc. (Richards, 2017). For the double-agent complex, Cohn shows progressions that tonicize each of the four members successively, and even those that do not tonicize any of them.²² Proto-harmony and component keys, according to Miasoedov and Dahlhaus respectively, are the most “egalitarian” of these complexes. An in-depth exploration of the idea of a harmonic complex is outside the scope of this paper; but the possibility of such an idea shows that certain features of proto-harmony are relevant to repertoires other than Russian liturgical music.

The relationship between proto-harmony and component keys (Teiltonarten) deserves attention, both because of its hierarchical flexibility as well as the issue of diatonicism versus chromaticism. The notion of component keys is discussed by Dahlhaus (1990 [1966]) in connection with Monteverdi’s madrigals and their transitional historical placement between modal and tonal eras.²³ The idea of component keys is based on the Guidonian hexachord.²⁴ Example 10 presents side by side the chordal roots of the proto-harmonic and the component-keys complexes, in two forms: (a) as a segment of the circle of fifths, and (b) as a scale. As a circle-of-fifths segment, the hexachord symmetrically extends the tetrachord by one fifth on either side.²⁵ As scales, they are also symmetrically related: the tetrachord lacks the hexachord’s central semitone (the mi–fa of the solmization tradition). This parallel with Dahlhaus’s ideas suggests a possibility that Miasoedov never acknowledges—that proto-harmonic structures may occur outside of Russian repertoire. For example, Monteverdi’s madrigal “Dunque Amate,” discussed by Dahlhaus, exhibits as its cadential plan the group C–G–D(d), which is a partial PH complex. But there is more interest for us here than this unexpected tonal similarity of very different repertoires. Of even greater importance is Dahlhaus’s suggestion that a chord which belongs to a diatonic group such as Teiltonarten can acquire chromatic notes on the musical surface. I now wish to suggest the same possibility for proto-harmony.

If chromatic alterations of both proto-harmony and component keys are possible, what is the need for a painstaking explanation of their diatonic origins? The answer, I argue, lies in the relationship of an underlying structural basis to local harmonic progressions. In Classical tonality, for example, the leading tone in minor does not change its theoretical collectional proximity with the relative major and other keys. Local harmonic syntax and chord quality do not affect the abstract form of natural minor that defines relationships with other keys. In much the same way, Dahlhaus’s component keys allow for local chromatic alterations of chords (triads with a Picardy third in cadences) that retain their abstract diatonic relationships with other hexachordal members. Proto-harmonic chords also may acquire chromatically altered tones without losing their membership in a diatonic PH complex. The main difference is that, for Dahlhaus, the chromatic variants of underlying diatonic chords result from their tonicization (though Dahlhaus does not use the term), while in Russian church music, surface chromaticism usually stems from dominantization (for example, see the D chord as V of G in Example 1a). If understood from a tonal viewpoint, the chromaticized chord locally functions as V of ii in major, which one can explain as “mutability of the second” (sekundovaia peremennost’)—that is, paired centers related by the interval of a second, here F major and G minor.

Chromatic variants of proto-harmonic members are featured in some of Miasoedov’s own examples, although he does not give a consistent explanation for the phenomenon. One such example is the main theme of Rachmaninoff’s Symphonic Dances (not shown), where the F-minor chord of the PH complex B$$\flat$$–c–E$$\flat$$–f is chromaticized as F major with a 7^th and a 9^th. Another example (Miasoedov’s Example 40) implies that the PH complex C–d–F–g contains a D-major chord, described as “preserving the diatonicism of harmony, in spite of the ‘accidentals’” (Miasoedov 1998, 50); this is the same situation that occurs in my Example 1.

To give a brief summary: the above study of proto-harmony from scalar, set-theoretical, and Neo-Riemannian viewpoints not only contextualizes the proto-harmonic group with respect to non-Russian theories. This study also allows us to see the internal structural balance of proto-harmony and to understand the proto-harmonic group as closely related to other groups, or harmonic complexes, similar to it with respect to harmonic relationships and hierarchical flexibility.

3. Proto-Harmonyand Form in Rachmaninoff’s Vigil

The remainder of this article is focused on two movements from Rachmaninoff’s All-Night Vigil. Here, I wish to address an aspect of proto-harmony that, in my view, needs the most development: the idea of structural equality among PH members at large levels; or, to use a Schenkerian term, as middleground harmonies. If the chords of a PH complex are inherently equal in status, as Miasoedov claims, they should be able to produce pieces decentralized from a Germanic-centered view of tonality. Specifically, I argue that, if the chords at phrase beginnings and endings belong to a single PH complex, one can see the piece as structurally unified according to proto-harmonic logic, as opposed to conventional tonal logic (which would require a single unifying tonic). This argument, of course, presupposes unambiguous phrase boundaries.

This is precisely what happens in the two hymns to be analyzed below: in each case, a partial PH complex manifests itself as a set of important formal pillars. I claim that the defining formal elements in this respect are two: (1) the framing harmonies at two levels—the entire movement and the individual phrase; this criterion thus includes all cadences, or cadential arrivals, to use Caplin’s term (1998); and (2) the chords that appear in cadential progressions.²⁶ Whichever harmonies participate in these areas comprise the PH complex at work.

The last of these criteria—the cadential progression—may require further discussion. Why should the chords that help produce a cadence be so important, and how many chords should one consider significant in this way? In the absence of a theory of cadences specific to Russian church music, my idea relies on the cadence classification accepted in the Western common practice. For the authentic cadence, as well as the plagal cadence (the importance of which grew as the nineteenth century progressed), the minimum requirement includes two chords—either V–I or IV–I, with possible additions such as V⁷ and IV^add6 (=II$$6\atop5$$).²⁷ Both harmonies in a cadential progression are considered structurally important, either for functional reasons (both D and S are primary tonal functions, according to Riemann’s theories) or for voice-leading reasons (e.g., the background dominant in a Schenkerian graph).²⁸ For the repertoire discussed here, I adopt the same view—that the last two chords of a cadential progression possess special significance.

I thus offer a somewhat simplified form-functional perspective in the sense that beginnings and endings of musical units perform a crucial structural role.²⁹ Ideas of monotonality—and thus non-monotonality—in fact, always have to do with beginnings and ends. When Carl Schachter (1999) sets off to discuss Chopin’s Fantasy op. 49 as monotonal (rather than directionally tonal), he argues that the movement begins off the tonic, but ends on the tonic, A$$\flat$$ major. Opposite approaches to such situations, approaches that prefer a directionally tonal view, also engage the beginning/end question. When Russian theorists, including Igor Sposobin, Yuri Kholopov, and Miasoedov, describe mutable structures in Russian music, they show how a folk song or church hymn may project one center (tonic) at the beginning and another one at the end. And since beginnings and endings ultimately articulate formal organization, the idea of one—or more than one—tonal center is inextricably tied to form.

But cadences and boundary points alone do not give us a complete picture; it is also important to trace the tonal processes within individual strophes, especially with respect to the shifting tonal/modal centers and their interaction. Although no rigid syntax operates in a PH complex, local progressions can nonetheless project one center stronger than another—a perception rooted in the modern (Western) listener’s tonal intuitions. Such intuitions cannot be reduced to a simple set of rules; one needs to penetrate the musical fabric with utmost possible attention to detail. In the examination of these processes, I use several additional viewpoints, in addition to proto-harmony: Riemann-based harmonic function, mutability (in close conceptual proximity with tonal pairing), and Schenkerian analysis. The goal is to show that a proto-harmonic view explains large-scale tonal openness (a “disunity” in a classical view of tonality) in a way that other methods cannot, and thus complements our understanding of structural integrity in these specific musical situations.

The use of Schenkerian techniques may need a justification. My Schenkerian graphs are meant to show what does not work from this viewpoint (and works well from a proto-harmonic perspective). But a voice-leading analysis is also useful because it allows for a close reading of the music using tools familiar to most North American readers. And, after all, certain elements of the music “work” perfectly well in Schenkerian terms; see, for instance, the fifth-progression in the first three strophes of movement 1, or the auxiliary cadence at the opening of movement 14.

To return to my analysis of form in the two Vigil movements: the form is modified strophic in both.³⁰ The musical phrases are not exactly the same, but every strophe of the text is set to music that has a recognizable shared basis. This shared basis is especially apparent at the beginnings of strophes, which are nearly equivalent throughout each of the movements. The clarity of formal divisions is ensured by the structure of text: each poetic strophe of the hymn corresponds to a musical phrase, with a firmly delineated opening and ending.³¹ Rachmaninoff’s original score of movement 1 reinforces this correspondence by placing bar lines only between phrases; no time signature or metrically regular measures are provided.³²

Before I proceed to the analysis proper, a brief overview of All-Night Vigil is appropriate. This a cappella choral work was written and first performed in Moscow in 1915. Stylistically, the work belongs to what Vladimir Morosan (1986) has termed the New Russian Choral School, a massive output of mostly sacred choral music by composers associated with or influenced by the Moscow Synodal Choir, which premiered Rachmaninoff’s Vigil.³³ The work sets fifteen hymns of the ordinary of the Russian Orthodox vigil service, consisting of two large sections—the vespers (movements 1–6 in Rachmaninoff) and the matins (movements 7–15). The movements that interest us are no. 1, which opens the service, and no. 14, which precedes the triumphant C-major final number. Of the fifteen hymns, these two are the most unusual from the standpoint of tonality, although elements of tonal disunity occur in other movements as well, notably nos. 2 and 12, both of which pair relative keys. Movement 14 uses a chant melody (Znamenny chant), whereas movement 1 does not.

3.1 Movement 1: “Priidite, Poklonimsia” (Come, Let Us Worship)

Examples 11 and 12 present the score and a formal overview of movement 1. The text, in English translation below the score, consists of four strophes of varying length, all with roughly the same meaning—a call for worship.³⁴ The formal chart in Example 12 shows the opening and closing harmonies of each strophe, as well as potential cadence labels according to the standard cadence classification in tonal music: three half cadences in D minor and a final cadence that is, at least potentially, a plagal close in G major. (Naturally, the final cadence produces the greatest analytical problems for the movement.) Here, the reader may well foresee my ultimate argument—that all the cadential harmonies belong to the PH complex G–A(a)–C–d, which thus governs the movement. At this point, however, I would like to take a step back and discuss the piece as if the concept of proto-harmony did not exist. This will help us explore the music from multiple perspectives and ultimately see the unique advantages the idea of proto-harmony offers.

How is one likely to hear this movement from a tonal perspective? At least two different explanations have been attempted. Vladimir Morosan and Alexander Ruggieri (1992, v) suggest that the movement is in C major, presumably because there are no accidentals in the key signature, and the first chord, separated from the following music by a double bar line, is the C-major tonic.³⁵ Musically, the C-major view makes more sense with respect to the whole Vigil (which begins with a C-major triad and ends with a solidly tonal C-major movement) than to the first movement alone, where the control of C major is rather limited. Ildar Khannanov, in his recent book about Rachmaninoff (2011, 17) states that it is “probably” (skoree svego) in A major. This interpretation is much more representative of the hymn’s musical behavior, but it too suffers from omissions; namely, it does not explain the C–G final cadence. A more satisfactory reading in conventional tonal terms would be a pairing (mutability) of C major and D minor, creating a considerable degree of ambiguity.³⁶ Example 13 presents the tonics and dominants—or primary and secondary mutable centers, to use Daniil Zavlunov’s (2010) expression—of the paired keys, C major and D minor. Seen differently, this example presents the four members of a complete PH complex, somewhat problematic for reasons of chromaticism: notice the presence of C$$\sharp$$.

Let us examine the hymn from the perspective of tonal mutability. The opening of strophe 1 emphasizes V of D minor, with a brief but important tonic upbeat: it is this upbeat that tells us the A is not a tonic harmony, or at least problematizes such hearing. The V of D minor dominates for four measures, upon which a short resolution to the D-minor tonic is followed by a tonicization of the second, rivaling the center of C major. C major gets a solid V–I progression, which could in fact be a cadence (PAC in m. 6). Such a cadence would create a D-minor/C-major pairing at the level of the strophe, with the balance tipped in favor of C major due to a strong cadence on the tonic (D minor receives much more emphasis on its dominant, rather than tonic). This, however, does not happen. Instead, Rachmaninoff somewhat unexpectedly returns to V of D minor to provide a half cadence. For the time being, therefore, the D center overrides the C, since the dominant of D minor begins and ends the phrase.

In a Schenkerian sense, strophe 1 prolongs the A-major harmony. Schenkerian analysis of proto-harmonic structures may require a separate study, but certain passages in the present movement lend themselves to linear analysis relatively easily. Strophe 1 is one such passage, thanks to the framing role of the A harmony and to the continuity of the upper line moving from E down to A. Example 14 presents this motion as a fifth-progression composing out the A triad throughout the strophe. The upper line is accompanied by a sixth progression in the alto from A down to C$$\sharp$$ (the alto 2 part in the choral score, to be specific). Notwithstanding the appearance of a C-major harmony at a middleground level, the background prolongs an A major, not minor, chord. The C$$\natural$$/C$$\sharp$$ dialectic can be explained using David Damschroder’s (2010, 29) term “wobbly note”: the alto’s C$$\sharp$$ at a deeper level is temporarily inflected to C$$\natural$$ and placed in the outer voices (m. 6), but it returns in the alto part at the end.

The subsequent two strophes expand the C-major tonicization in the middle of the phrase. In strophe 2, the textual phrase “Tsarevi nashemu Bogu” acquires a new word—“Khristu Tsarevi etc.,” and the C-major passage in mm. 11–15 is here longer and more elaborate than before. It even includes an internal mini-excursion back to D minor, mm. 13–14 (but without accidentals). Strophe 3 enriches the music with another tonicization, G minor, before once again tonicizing C major (mm. 23–25) and returning to V of D. The rivalry of the two paired global tonics, C major and D minor, is most apparent in this strophe.

The final strophe, however, invalidates the prolongation of the A harmony and with it the fifth-progression in the upper voice. The phrase opens the way all previous phrases do, but “gets stuck” in the C-major tonicization and ends up on its dominant G, thus producing a HC within the C-major tonic. Thus, neither of the two competing centers gains full tonal control. Instead, the piece ends as if in hesitation (mark the pianissimo dynamic!), in awe of its own extraordinary tonal course.³⁷ This sense of hesitation continues in the next movement, which vacillates between C major and A minor, a classic example of relative mutability (that is, pairing of relative keys).

Matters are further complicated, of course, because the phrase beginnings and endings articulate paired dominants, not tonics. The dominantized character of the A chord especially creates expressive intensity that makes the hymn something more than just a call for worship, something nearly tragic; this mood is further reinforced by the descending (“lament”) melodic phrase endings. Two concepts come to mind in connection with this dominantization: first is Kholopov’s “dominant mode” (dominantovyi lad), which refers to dominant emphasis that substitutes for tonic emphasis and involves final cadences on V. Second is Bailey’s “double-tonic complex,” which he proposed for paired tonics in Wagner’s Tristan, and which in this case may perhaps be modified to a “double-dominant complex.” On the other hand, the two centers A and G may perhaps be considered tonics, rather than dominants. The two chord pairs A–d and G–C would then be plagal, and the A and G tonics then receive a Phrygian and Mixolydian character, respectively.³⁸ (The coexistence of B$$\natural$$ and B$$\flat$$ may stem from the obikhod collection; revisit Example 4.) This structure would result in Example 13 with the internal relationships flipped: the dominants become tonics, and the tonics become subdominants. The interval of pairing—major second—remains unchanged. This hearing receives particular support in the final cadence, mm. 33–34: the stepwise ascent G–A–B in the second tenor creates a pattern recognized as early as Rameau (in his Traité; 1971 [1722]), who calls it cadence imparfaite or irregulière, and known now as the prototypical plagal progression.

As unusual as this music may be from a tonal-functional viewpoint, the explanation in terms of mutability/tonal pairing makes some sense. In Schenkerian terms, however, strophe 4 and the whole movement is practically unjustifiable. Given the soprano motion from the much-emphasized E to the final B, any prolongational logic is excluded. This “false”—or perhaps abandoned—linear progression would suggest a prolongation of E major or minor, a harmony completely absent from the music.³⁹ One can see this false linear progression in Example 15, an analysis of the upper voice alone, showing the extent to which the upper line is at odds with prolongational harmonic principles.⁴⁰ The example uses melodic reduction to “straighten out” the melody into an underlying stepwise line. The melodic behavior of the last strophe clarifies its conflict with the harmonies projected by the full choral texture. By contrast, the remarkable continuity of the melody, slightly reduced in this analysis—on the surface, it is completely stepwise—counterbalances the incoherence of the attempted prolongational view.

One can, of course, attempt a Schenkerian background reading of the final strophe and the whole movement, even if this required some methodological compromises (since it is hard to imagine a reading that would represent the movement properly prolonging a single harmony); refer to Example 16. But none of these attempts is satisfactory. If one assigns a true tonic status to the D-minor chord in strophe 4 (m. 28) and reads it as the structural close, then everything after it is post-structural; the events prior to m. 28 would be a huge auxiliary cadence.⁴¹ This does not work because m. 28 is obviously not a cadence; in fact, it falls in the middle of a word (poklonimtisia) in all voices. A somewhat more appealing option is to take the D-minor and G-major chords as structural, thus demoting the opening A to a subordinate status. This, in my view, is also flawed, not only because the D chord is hardly structural (see above), but also because the A harmony is arguably continued from the preceding strophes, where it was properly prolonged, and is thus very important. Besides, this background would involve an immovable upper tone D, rather than a structural descent of any kind. A background C–G progression also fails to emphasize the A chord; and an A–G progression completely lacks any Schenkerian justification, since the two chords do not even share any tones. Finally, one might be tempted to ignore the final strophe entirely, deciding on a prolongation of the A harmony throughout strophes 1–3, with strophe 4 as a kind of post-structural tail, quite literally a coda. This, however, conflicts with the strophe’s opening, equivalent to the preceding three openings, which hardly allows for a coda-like hearing.

While some readers may prefer, to a certain extent, some of the options described above, I argue that the compromises are too great in all of them. The structure simply defies a Schenkerian reading, offering instead the kind of equality of status among the participating chords that Miasoedov seems to advocate—an equality fundamentally incompatible with Schenkerian analysis. Thus, having explored the harmony of “Priidite” from multiple perspectives, let me now return to the idea of proto-harmony.

A review of Example 12 reveals that the harmonic pillars of the piece together form the PH complex G–A(a)–C–d. The majorized A triad stands in for the a-minor chord of the underlying diatonic complex (see a justification of chromatic variants within a PH complex in the earlier theoretical section of this article.) Deciding whether there is a complete or partial PH complex at work may well depend on subjective judgment. If one prioritizes the prolongation of A plus the final C–G cadence, a partial complex G–A(a)–C results; this is my preferred view. If, however, one includes the initial two-chord progression d⁶–A (just as we include the two-chord cadential segment), a complete PH complex results. This latter view may also be buttressed by (paleo-)Riemannian harmonic considerations: the tonic-dominant (or subdominant-tonic!) relationship of the d and A harmonies, clearly expressed in the music, suggests equal structural rights for these two harmonies.⁴²

A proto-harmonic view does not override or replace the other—harmonic-functional and linear—views; these two perspectives still illuminate important musical elements and, most significantly, express ways in which Western listeners are likely to hear this music. But a proto-harmonic analysis effectively addresses several problems that no other perspective is likely to solve:

1. It explains the structural origin of this particular tonal pairing, C major/D minor;
2. It offers a view of several harmonies as being hierarchically equal, rather than creating a picture of incompleteness (recall the “abandoned” linear progression in strophe 4);
3. It reveals that the movement, in fact, is internally unified through the common proto-harmonic membership of formal-boundary harmonies, rather than rife with rivaling tonal tendencies.

From a form-functional perspective, this internal unity is especially relevant to the concluding phrase, which decentralizes the movement from non-proto-harmonic viewpoints. The G chord is the only de-emphasized PH member throughout the piece; it appears only as a local dominant in C-major tonicizations in phrase middles (Caplin’s medial function). To use Miasoedov’s social metaphor of equality: The highest level of formal hierarchy, by placing the G at the final cadence, interferes at the end to restore the proto-harmonic balance that the lower levels failed to provide. This highest level, therefore, reveals that the rivaling keys C major and D minor are expressed only due to locally “normal” harmonic syntax. The big picture arises from another, non-tonal principle—proto-harmony.

To summarize, my analysis has demonstrated that the movement is generated by the partial PH complex G–A(a)–C, with the A chromaticized to become major. Two structural elements of the music project this complex: the boundary harmonies and the cadential plan (according to the criteria discussed above), and the pairing of two second-related keys, C major and D minor. The proto-harmonic basis dominates at the largest level of structure, but the normalcy of harmonic syntax creates the possibility of interpreting the music in traditional tonal terms. A proto-harmonic analysis enables one to understand that the movement is internally unified, while harmonic-functional and linear analyses both create a picture of a disunity or at least a significant deviation from the norm.

3.2 Movement 14: “Voskres iz Groba” (Risen from the Dead)

Movements 1 and 14 have much in common. Like the first one, the fourteenth, “Voskres iz groba,” presents difficulties with regard to key and/or mode identification. Both movements also begin and end on different harmonies, which are, in the case of movement 14, diatonically related: D minor and G major. But, unlike “Priidite,” this movement is mostly in the natural system; a few accidentals occur mid-phrase but do not affect formal-boundary harmonies. On the largest scale, therefore, chromaticism is embellishing rather than structural.

It is, perhaps, for this reason that this hymn is more easily explicable in monotonal terms than is movement 1. One can conceivably understand and hear it in C major throughout, primarily thanks to several strong cadences in this key, although such a hearing would involve a non-tonic beginning and ending, similar to those in my Example 1. And yet, in the remaining portion of this paper, I will argue that important aspects of the piece, including chant-related ones, are lost in such a reading. Instead, I show that proto-harmony lies at the basis of this movement, built on a partial PH complex C–d–G. The complex is expressed through formal boundaries, cadential plan, the chant structure, and the internal harmonic content of each phrase, particularly the first, which encompasses all three crucial chords of the piece.

The four-strophe movement is based on a Znamenny chant, provided mostly in the soprano and sometimes, partially, in other voices (bass and tenor). Example 17 gives the score of the movement (piano reduction only), and Example 18 presents a formal chart. Again, like movement 1, this movement is in a modified strophic form. Melodically parallel phrase beginnings and internal content become increasingly extended and elaborate with each new phrase, and the last cadence abruptly departs from the cadential pattern established in previous phrases. The cadential plan shows two straight-forward PACs (mm. 7 and 19) concluding strophes 1 and 3, an elided PAC (m. 12), and a final cadence on G, possibly a HC. This final cadence will shortly be discussed more extensively.

Harmonically, the first two strophes follow the same basic trajectory. The first strophe is the shortest and simplest: it articulates a ii–V⁷–I progression in C major. The repeated ii–V motion will become motivic later in the movement, giving the D-minor chord a distinctly Dorian flavor—every time, it sounds potentially like a tonic, as at the beginning. But B$$\flat$$ also occurs (m. 5), and its coexistence with B$$\natural$$ calls to mind the obikhod collection. In Schenkerian terms, the phrase represents an auxiliary cadence. Strophe 2 is longer and contains the first true tonicization: D minor is tonicized with the B$$\flat$$ and C$$\sharp$$, although no V of D ever occurs. Thus, a now familiar element is introduced here—mutability of a second; recall the same mutability type in movement 1. The PAC, expected in m. 12 (the end of strophe 2 in the chant), is elided thanks to the bass omitting the cadential C and asserting the opening strophe 3 of the chant instead. Strophes 2 and 3, therefore, overlap in time.⁴³ Strophe 3 is perhaps the most “tonal,” syntactically speaking. It tonicizes two different harmonies, A minor and D minor, with proper tonal progressions in both (see the score), and a PAC in C major. Strophe 4, however, destroys the illusion that we are moving in the direction of increasing tonal stability. It brings back the fluctuation between D minor and G major chords and, in addition, introduces the ostensibly unusual D$$4\atop2$$ (ii$$4\atop2$$ in C major) with leaps to and from the chordal seventh in the bass. The following lengthy cadential progression in C may seem to “repair” the situation by reasserting the C center, with another PAC. The last five measures, however, complicate things again by concluding the movement on a G chord.

It is this ending that reveals more about the piece, and it requires more explanatory effort than any preceding events. It is also here that one has to decide (if one insists on a decision at all) whether a monotonal interpretation of the movement is possible. The main question is, where does the true final cadence arrive, in m. 26 or 31? For those who prefer hearing the piece in one key, it is tempting to hear the PAC at m. 26 as the true structural end, with a post-cadential tonic pedal that, for some reason, leads to a V chord. Of course, this creates a picture of the movement that begins and ends on non-tonic chords: the piece opens with a ii harmony and ends on V. But, given the strength of the PACs, as well as the syntactical and voice-leading normalcy of the middle strophes, a C-major view of the hymn is viable. A monotonal Schenkerian reading of the piece would probably look something like Example 19, with an auxiliary cadence at the start and a post-structural digression at the end. One could potentially call this ending a fifth divider, if it wasn’t the end of the movement.⁴⁴

I will not argue that this view is invalid. But, at least one, chant-related aspect problematizes it. This aspect has to do with the structural end. Viewing m. 26 as the true close definitely makes tonal sense, and to a certain degree even textual sense: the grammatically complete sentence is over at the cadential arrival at m. 26, with the last word Mno-gomilostive (“the most merciful one,” addressed to Christ) as indeed post-structural. What is not taken into consideration in the monotonal C-major reading is the chant. At this moment, it is appropriate to offer a brief analysis of the chant melody and to then relate it to Rachmaninoff’s arrangement.

Example 20 partially presents the chant melody. The example shows the first cadence on C, which is then reiterated twice more (not shown). These cadences translate into PACs in Rachmaninoff’s harmonization, except the elided cadence in m. 12. With respect to its modal structure, the first strophe displays a definite pitch center—an ustoi—on D. At the cadence, the center shifts to C, thus producing modal mutability of a second between D and C. Importantly, however, the final cadence does not repeat this D–C motion. Instead, it returns to D, thus solidifying the ustoi suggested at the beginning. The melody is thus unified by a single center D, the other center C being structurally subordinate. To use Western modal terms, the chant is in D Dorian, with D as a final and A—the opening note—as a cofinal.

It is this structure of the chant that is at odds with a C-major view of the movement. The “PAC” in m. 26, corresponding to the half note E of the chant’s last line, is problematic for several reasons. First, it is not a phrase ending because the following material is not a phrase beginning, parallel to all the other beginnings (that is, not an ascending tetrachord). Second, even if it was a phrase ending, it articulates E rather than C, which arguably weakens the PAC in m. 26 (potentially makes it an IAC), since all the other PACs contain a chant note C in the soprano.

With the above discussion in mind, I offer my final reading of the movement as fundamentally proto-harmonic, built on the partial PH complex C–d–G (return to Example 18), whose complete form would be G–a–C–d. This partial complex is projected by important formal boundaries. The C-major and D-minor harmonies represent the beginning and end respectively, and C major generates the internal cadences. The missing harmony that would complete the PH complex, A minor, is present in internal progressions (that is, by the medial formal function; see the A-minor tonicization in strophe 3, for instance), as well as the elided cadence in m. 12. Thanks to the phrase overlap here, the A-minor harmony becomes, in a way, a formal beginning and ending. Whether this makes it a legitimate member of the PH complex, which would then be complete, is perhaps less crucial.⁴⁵

Interestingly, if the true melodic close is the D, Rachmaninoff’s most obvious choice is to end the movement on a D-minor triad. This would have created a tonally closed structure in D Dorian, quite in line with the chant itself. One can only speculate as to why Rachmaninoff chooses to end on G instead. Let me suggest two of the possible reasons. One is that he intentionally makes the movement as unpredictable as possible and thus decentralizes it from a conventional tonal sense. (The following movement, in strong C major, compensates for this decentralization and suggests that the overall tonal center of the entire Vigil is C.) The other reason is primarily analytical; compositionally, it could only have been unconscious, based on Rachmaninoff’s intuitive knowledge of proto-harmonic structures. It is the idea to provide a balance within the PH complex at work. The partial complex C–d–G had been suggested in the opening phrase (then given in the order d–G–C), and, in a sense, the formal and cadential plan of the movement is an enlargement of this group. A final close on G, metaphorically speaking, restores justice with respect to this harmony, which was somewhat “overlooked” in the preceding music.

There remain two methodological questions to be addressed. The first concerns diatonic modes. One can justly ask whether one can interpret the movement as floating within a system of seven diatonic modes, that is, mostly between D Dorian and C Ionian, with a shift to G Mixolydian at the end. Isn’t this as good an explanation as a proto-harmonic one? My answer is “Yes,” but only to a certain extent. A modal view differs from a proto-harmonic one in that the music floats within a system of seven rather than four possible centers. Russian church music, for the most part, operates within this group of four, rather than seven, centers.

The second—and related—question is which conventionally understood cadence type each cadence represents. In movement 1, a similarly unexpected final cadence on G offers a dual possibility: one can hear it as a HC in C, or as a plagal cadence in G. In movement 14, the concluding d–G progression, while still allowing for a HC hearing, excludes the plagal possibility, suggesting instead a kind of Mixolydian IAC in G major. From a proto-harmonic viewpoint, however, the question may be somewhat inadequate. Since proto-harmony relaxes—or even withholds—tonal centricity and conventional syntactical norms, they arguably lose their significance in this context. Even the identity of the C-major PACs becomes less obvious, or at least less crucial, than it would have been in an unambiguously tonal work. Here, the cadences serve to shift the center from one PH member to another more importantly than they serve to articulate standard cadence types. (This said, the educated Western listener will probably hear these standard types nonetheless, at least when they are relatively unproblematic, such as that in m. 7.)

Conclusion

In this paper, I have explored two broad aspects of proto-harmony: (1) its structural properties as a theoretical construct and (2) its analytical application in several examples from Russian church music, with a focus on movements 1 and 14 from Rachmaninoff’s All-Night Vigil. The chords of a proto-harmonic complex obviously are not limited to Russian music, for which Miasoedov developed his concept; in fact, the complex, either complete or partial, occurs in many repertoires, tonal and beyond. It is for this reason that I have offered a more precise formulation of proto-harmony with respect to one of its central criteria, borrowed from Miasoedov’s own work: the potential of proto-harmonic members to serve as tonics—that is, the hierarchical flexibility that defines the harmonic complexes I have discussed. This potential is most evident, and most drastically different from common-practice tonality, when the use of PH members as large-scale structural pillars violates tonal unity by (1) placing different PH members at formal boundaries, including the extremes of entire pieces, and (2) problematizing conventional functional relationships and cadential formulas. If future research engages the possible applicability of proto-harmony to non-Russian repertoires, which I have attempted in my discussion of Dahlhaus and a Monteverdi madrigal, the central question to explore would deal with the issue of hierarchy at global structural levels. How exactly this issue can be played out in specific musical situations would seem to open unlimited horizons for theoretical and analytical work.

---

Ellen Bakulina is Assistant Professor of Music Theory at the University of North Texas, and a recent graduate of the City University of New York (2015). She has degrees from the College of the Moscow Tchaikovsky Conservatory (Russia), McGill University (Canada), and the City University of New York (USA). She has previously taught at McGill, CUNY, and the Yale Department of Music. Bakulina’s areas of interest include Schenkerian analysis, theories of form and meter in tonal music, the music of Sergei Rachmaninoff, and the Russian music-theoretical tradition. Her articles, besides the one in the present volume of Intégral, have appeared in several journals, including the Canadian journal Intersections, Music Theory Online, and the Journal of Music Theory.

References

Agmon, Eytan. 1989. “A Mathematic Model of the Diatonic System.” Journal of Music Theory 33 (1): 1–25.

Bailey, Robert (ed.). 1985. Prelude and Transfiguration from Tristan and Isolde. New York: Norton.

Bakulina, Ellen. 2014. “The Concept of Mutability in Russian Theory.” Music Theory Online 20 (3). http://www.mtosmt.org/issues/mto.14.20.3/mto.14.

———. 2015a. “Tonality and Mutability in Rachmaninoff’s All-Night Vigil, Movement 12.” Journal of Music Theory 59 (1): 63–97.

———. 2015b. “The Problem of Tonal Disunity in Sergei Rachmaninoff’s All-Night Vigil, op. 37,” Ph.D. dissertation, City University of New York.

Bertensson, Sergeĭ, and Jay Leyda. 1956. Sergeĭ Rachmaninoff: A Lifetime in Music. New York: New York University Press.

Burns, Lori. 1995. Bach’s Modal Chorales. Stuyvesant: Pendragon Press.

Burstein, L. Poundie. 2006. “Schenker’s Concept of the Auxiliary Cadence.” In Essays from the Third International Schenker Symposium, edited by Allen Cadwallader and Jan Miyake, 1–36. Hildesheim: Georg Olms Verlag.

Cadwallader, Allen, and David Gagné. 2016. “The Evolution of the Quintteiler Concept in Schenker’s Published Writings.” Music Theory Spectrum 38 (1): 109–117.

Caplin, William E. 1998. Classical Form: A Theory of Formal Functions for the Instrumental Music of Haydn, Mozart, and Beethoven. New York: Oxford University Press.

Cannata, David. 1999. Rachmaninoff and the Symphony. Innsbruck: Studien-Verlag.

Christensen, Thomas. 2017. “Dahlhaus and the Origins of the Origins.” Theoria 24: 141–156.

Clough, John, and Jack Douthett. 1991. “Maximally Even Sets.” Journal of Music Theory 35 (1–2): 93–173.

Clough, John, and Gerald Myerson. 1985. “Variety and Multiplicity in Diatonic Systems.” Journal of Music Theory 29 (2): 249–270.

Cohn, Richard. 2012. Audacious Euphony: Chromaticism and the Consonant Triad’s Second Nature. New York: Oxford University Press.

Dahlhaus, Carl. 1990 [1966]. Studies on the Origin of Harmonic Tonality. Translated by Robert Gjerdingen. Princeton: Princeton University Press.

Damschroder, David. 2010. Harmony in Schubert. Cambridge: Cambridge University Press.

Frolova-Walker, Marina. 2007. Russian Music and Nationalism: From Glinka to Stalin. New Haven: Yale University Press.

Gauldin, Robert. 1983. “The Cycle-7 Complex: Relations of Diatonic Set Theory to the Evolution of Ancient Tonal Systems.” Music Theory Spectrum 5: 39–55.

Gosden, Stephen. 2012. “Rachmaninoff’s Branch of the Russian Oak: Rotational Form and Symmetrical Harmony in the Isle of the Dead and the ‘Intermezzo’ of the Third Piano Concerto.” Presentation at the Annual Meeting of the Music Theory Society of New York State, Hunter College, City University of New York.

Harrison, Daniel. 1994. Harmonic Function in Chromatic Music: A Renewed Dualist Theory and an Account of Its Precedents. Chicago and London: University of Chicago Press.

Hepokoski, James, and Warren Darcy. 2006. Elements of Sonata Theory: Norms, Types, and Deformations in the Late-Eighteenth-Century Sonata. New York: Oxford University Press.

Hyer, Brian. 2002. “Tonality.” In The Cambridge History of Western Music Theory, edited by Thomas Christensen, 726–752. Cambridge: Cambridge University Press.

Johnston, Blair. 2014. “Modal Idioms and Their Rhetorical Associations in Rachmaninoff’s Works.” Music Theory Online 20 (4). http://www.mtosmt.org/issues/mto.14.20.4/mto.14.20.4.johnston.html.

Khannanov, Ildar. 2011. Muzyka Sergeĭa Rakhmaninova: Sem’ Muzykal’no-Teoreticheskikh Etiudov [The Music of Sergeĭ Rachmaninoff: Seven Music-Theoretical Studies]. Moscow: Kompozitor.

Kholopov, Yuri. 1988. Garmoniia: Teoreticheskiy kurs [Harmony: A Theoretical Course]. Moscow: Kompozitor.

Kinderman, William, and Harald Krebs (eds.). 1996. The Second Practice of Nineteenth-Century Tonality. Lincoln: University of Nebraska Press.

Kustovsky, E., and N. Potiomkina (eds.). 1999. Posobie po izucheniiu osmoglasiia [A Manual for the Study of Oktoechos]. Moscow: Pravoslavnye Moskovskie Regentskie Kursy.

La Rue, Jan. 2001. “Bifocal Tonality: An Explanation of Ambiguous Baroque Cadences.” The Journal of Musicology 18 (2): 283–294.

Morgan, Robert. 2003. “The Concept of Unity and Musical Analysis.” Music Analysis 22 (1): 7–50.

Morosan, Vladimir. 1986. Choral Performance in Pre-Revolutionary Russia. Ann Arbor: UMI Research Press.

Miasoedov, Andrei. 1998. Garmoniia russkoy muzyki: korni natsionalnoj spetsifiki [Harmony of Russian Music: The Origin of the National Characteristics]. Moscow: Prest.

Murphy, Scott. 2014. “A Pop Music Progression in Recent Popular Movies and Movie Trailers.” Music, Sound, and the Moving Image 8 (2): 141–162.

Neuwirth, Markus. 2015. “Fuggir la Cadenza, or The Art of Avoiding Cadential Closure.” In What Is a Cadence? Theoretical and Analytical Perspectives on Cadence in the Classical Repertoire, edited by Markus Neuwirth and Pieter Bergé, 117–155. Leuven: Leuven University Press.

Nobile, Drew. 2017. “Double-Tonic Complexes in Rock Music.” Paper presented at the Annual Meeting of the Society for Music Theory, Arlington, VA, November 3, 2017.

Prussing, Stephen. 1979. “Compositional Techniques in Rachmaninoff’s Vespers, Op. 37,” Ph.D. dissertation, The Catholic University of America.

Rachmaninoff, Sergei. 1992 [1915]. Vsenoshchnoe bdenie (All-Night Vigil), Op. 37. Edited by Vladimir Morosan and Alexander Ruggieri. San Diego: Musica Russica.

Rameau, Jean-Philippe. 1971 [1722]. Treatise on Harmony. Translated by Philip Gossett. New York: Dover Publications.

Rothstein, William. 2008. “Common-Tone Tonality in Italian Romantic Opera: An Introduction.” Music Theory Online 14 (1). http://www.mtosmt.org/issues/mto.08.14.1/mto.08.14.1.rothstein.html.

Richards, Mark. 2017. “Tonal Ambiguity in Popular Music’s Axis Progressions.” Music Theory Online 23 (3). http://mtosmt.org/issues/mto.17.23.3/mto.17.23.3.richards.html.

Schachter, Carl. 1999 [1988]. “Chopin’s Fantasy, Op. 49: The Two-Key Scheme.” In Unfoldings, edited by Joseph Straus, 260–288. New York: Oxford University Press.

Schenker, Heinrich. 2004. Der Tonwille. Volume 1, issues 1–5 (1921–23). Edited by William Drabkin. New York: Oxford University Press.

Smith, Peter H. 2013. “Tonal Pairing and Monotonality in Instrumental Forms of Beethoven, Schubert, Schumann, and Brahms.” Music Theory Spectrum 35 (1): 77–102. Sposobin, Igor. 1994 [1951]. Elementarnaia Teoriia Muzyki [Elementary Music Theory]. Moscow: Kifara.

Stein, Deborah 1983. “The Expansion of the Subdominant in the Late Nineteenth Century.” Journal of Music Theory 27 (2): 153–180.

Straus, Joseph N. 2014. “Harmony and Voice Leading in the Music of Stravinsky.” Music Theory Spectrum 36 (1): 1–33.

Swinden, Kevin. 2005. “When Functions Collide: Aspects of Plural Function in Chromatic Music.” Music Theory Spectrum 27 (2): 249–82.

Tymoczko, Dmitri. 2011. A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice. New York: Oxford University Press.

Waters, Keith. 2016. “Chick Corea and Postbop Harmony.” Music Theory Spectrum 38 (1): 37–57.

Wadsworth, Benjamin K. 2012. “Directional Tonality in Schumann’s Early Works.” Music Theory Online 18 (4). http://www.mtosmt.org/issues/mto.12.18.4/mto.12.18.4.wadsworth.html.

Zavlunov, Daniil. 2010. “M.I. Glinka’s “A Life for the Tsar” (1836): a historical and analytic-theoretical study,” Ph.D. dissertation, Princeton University.

1. Glas hymns are roughly similar to psalm tones of the Roman Catholic tradition but are used differently. The hymns in Example 1 are borrowed from a 1999 collection of church hymns (Oktoechos), edited by Kustovsky and Potiomkina, currently in wide use by the Russian Orthodox Church. The anonymous hymns are remnants of Old Russian chant traditions harmonized in four voices. Although the collection was published in 1999, its harmonization style reflects nineteenth-century and earlier traditions (Kustovsky/Potiomkina, 1–5). See Stephen Prussing 1979, Vladimir Morosan 1986, and Ellen Bakulina 2015b for the history of Russian chant and its fate in the nineteenth and twentieth centuries.
2. Throughout this paper, I use the Library of Congress system of transliteration from Russian into English, excepting names, such as Rachmaninoff, that have an established English spelling.
3. See William Kinderman and Harald Krebs 1996, Jan La Rue 2001, William Rothstein 2008, Benjamin Wadsworth 2012, Peter Smith 2013, Drew Nobile 2017, and Keith Waters 2016, among others. The term “tonal pairing” originates in Robert Bailey’s writings (1985). In Rachmaninoff, tonal pairing has been discussed by David Cannata (1999) in the symphonies, Bakulina (2015a) in sacred music, and, to a certain extent, by Blair Johnston (2014), who discusses diatonic co-centers as a subcategory of “limited pandiatonicism.”
4. The idea of structural unity may generate some controversy of the kind Robert Morgan (2003) engages in. Without engaging the philosophical issue of unity as a concept, I adopt a—perhaps somewhat simplistic—view of unity as an element that holds a piece together, such as a key in tonality or a twelve-tone row in dodecaphony. This view is generally in line with “the Schenkerian and Schoenbergian traditions, committed—as Webern puts it—to the demonstration of the ‘utmost relatedness between all component parts’,” in the words of the editorial introduction to Morgan’s article.
5. Examples include his rather critical references to Hugo Riemann and Riemann-based Russian/Soviet harmony textbooks (see Miasoedov 1998, 31 and 130-31). Towards these textbooks, his attitude is almost hostile.
6. His reference to O. and S. Skrebkovs’ anthology for harmonic analysis is representative (Miasoedov 1998, 130).
7. Like other Russian theorists, Miasoedov uses the word “harmony” to mean something close to what “tonality” means in English, to refer to an abstract system of relationship between pitches (see Brian Hyer 2002, 727–28). This is the first meaning in Carl Dahlhaus’s article of the term “harmony” in the New Grove dictionary.
8. To do full justice to the treatise, I must add that proto-harmony is not the only topic Miasoedov discusses. He touches upon other topics, such as functionality understood in Riemann’s sense, “plagalism” (the importance of plagal structures in minor), the origins of minor in the overtone series, and the so-called “all-scale-degree harmony” (vsestupennost’), which means that all chords in a certain collection are equally important.
9. The four chordal roots of proto-harmony coincide with what Joseph Straus (2014) calls bi-quintal harmony, model 2; on the intervallic level, this model include two fifths a major second apart, or C–G and D–A. One can speculate that the use of model 2 in Stravinsky originates in proto-harmonic structures of Russian folk music.
10. Interestingly, Miasoedov does not pay attention to the perfect-fifth coordination of the three central triads of classical tonality, I–IV–V, as formulated by Jean-Philippe Rameau and later theorists, as well as II–V–I.
11. When speaking about “tonic,” Miasoedov frequently uses the word ustoi, which has no direct equivalent in English. It can be roughly translated as “center,” although etymologically it is related to “stability” (ustoichivost’). Ustoi is a standard term for modal/tonal center in Russian ethnomusicology. For monophonic analyses in terms of ustoi/neustoi (stable and unstable tones), see Kholopov 1988 (173–188).
12. I have explored in depth the Russian theories of mutability elsewhere (Bakulina 2014 and 2015a and 2015b). Here, it is important to remember that (1) the term mutability is applicable to both modal (pre-tonal) and tonal contexts, and (2) that mutability is not limited to any specific kind of key relationship, for example relative. Miasoedov mentions mutability only in passing (see p. 19, for instance) and regards it as a kind of side effect of proto-harmony.
13. To say, however, that two members of a PH complex suffice to form a partial complex seems highly dubious. Instead, let me suggest that such a pair can point to a fuller proto-harmonic group (of at least three members) that underlies a certain passage or movement.
14. Miasoedov often uses Roman numerals (see his Chapter 2, for instance), even when he clearly deals with a pre-tonal musical universe. Letter notation does not appear in his treatise.
15. Other studies of diatonicism that involve set theory and other mathematical methods include Eytan Agmon 1989, Clough and Myerson 1985, Clough and Douthett 1991, Tymoczko 2011, and many more.
16. This thinking is very much in line with Miasoedov’s, who also generates diatonic scales of any type by ordering tones in fifths, and who also uses ethnomusicological data for historical and theoretical claims.
17. The term obikhod in music has several meanings. It can mean a set of church hymns particular to a certain regional tradition or even a specific parish; it can also mean a printed collection of such hymns (see Kustovsky and Potiomkina 1999 on the history of printed obikhods). Obikhod is a pc collection formed in Old Russian (that is, pre-Westernized) church music. Pitch-class-wise, the obikhod collection is equivalent to the medieval gamut.
18. As a side note, the PH complex and the obikhod collection are complementary set classes, as seen on Gauldin’s table, Example 3.
19. See Miasoedov 1998, 9–10, for his discussion of the obikhod collection. The example also shows the perfect-fourth recurrence of the PH complex as a chain of interlocking groups (if we extend the obikhod collection to include E$$\flat$$). Each pair of such groups, which includes six individual chords, is what Miasoedov (21) calls extended proto-harmony.
20. The term “harmonic complex” was suggested to me by an anonymous reader.
21. According to Miasoedov, proto-harmony is also a chord-to-chord progression, although without a fixed order. My claim, in the next section, that members of a PH complex can function as middle-ground harmonies is distinct from Miasoedov’s idea.
22. One can object that, in the Classical functional group T–S–D, one can also tonicize them all, and that, therefore, the T–S–D group may qualify as a harmonic complex. The difference, however, is that the global center for a piece is normally fixed on the T, whereas, in the double-agent complex, at least two members—the R-related pair—are equally viable global tonics.
23. The idea of hexachordal component keys originates with Siegfried Hemerlink, whose ideas Dahlhaus (1990 [1966]) engages. See Thomas Christensen 2017 for more on Dahlhaus’s exploration of the origins of tonality.
24. Miasoedov mentions both the hexachord and the pentatonic scale in his Chapter 1, although he does not make a connection with the Western musical tradition. Among the many conceptual similarities between proto-harmony and Teiltonarten, let me mention that both use social metaphors (Dahlhaus’s component keys are “a closed society,” and Miasoedov’s proto-harmony is akin to the rivalry of medieval princes, p. 21), and both strongly emphasize structural equality.
25. The reason the extension is symmetrical—one perfect-fifth step in each direction, rather than two such steps in one direction—has to do with triad qualities. If the hexachord extends the tetrachord up by two fifths to E and B, or down to F and B, the B triad will be diminished.
26. These criteria are necessitated by Miasoedov’s argument that proto-harmony requires no definite syntax and no overarching tonal center. In the absence of these two aspects, so basic for classical tonality, formal boundaries acquire even more structural significance than they do in Western tonal music.
27. The half cadence, the least conclusive of all, is the only type whose minimum requirement is a single chord, V, which can be preceded by virtually anything. Had there been a defined hierarchy of cadence types in Russian church music (apart from the cases which obviously qualify for an established classical type), one would have more grounds to decide just how many chords should be considered structural in each specific cadence type.
28. The same has been done with a background IV, which, according to certain commentators, may at times replace V and thus produce a plagal fundamental structure; see, for instance, Lori Burns (1995), who proposes plagal Schenkerian backgrounds for Bach chorales in the Phrygian mode. The importance of IV has been discussed by Deborah Stein (1983); Daniel Harrison (1994); and Kevin Swinden (2005). On plagalism in Russian music, see Daniil Zavlunov 2010 (468) and Marina Frolova-Walker 2007 (106-107); Miasoedov’s discussion on this topic concerns the minor mode more often than major.
29. My form-functional view is simplified in the sense that Caplin’s (1998) theory of formal functions focuses on three (not two) functions: initial, medial, and concluding, whereas my analysis mostly concentrates on the outer functions, initial and concluding. In addition, Caplin has a highly nuanced classification of harmonic and other events with respect to the three functions, an endeavor hardly possible for Russian church music.
30. According to Michael Tilmouth’s definition in Grove Music Online, the term strophic form is “applied to songs in which all stanzas of the text are sung to the same music, in contrast to those that are through-composed and have new music for each stanza.” All fifteen movements of the Vigil exist somewhere on a continuum between strophic and through-composed forms, although none of the pieces belongs to either of these pure types. Movement 1 is closest to the pure type; movements 7 and 12 are perhaps the furthest from it. In chant-based movements, the form depends on how much strophicity the chant melody exhibits. Strophic form can be also understood from a rotational perspective (as developed in the theory of Hepokoski and Darcy 2006). On rotational forms in Rachmaninoff, see Stephen Gosden 2012.
31. In the two hymns to be analyzed here, phrase boundaries are completely unequivocal and consistently aligned in text and music. Not all movements in the Vigil, however, exhibit the same degree of correspondence between textual and musical units; no. 5, for example, is more complicated.
32. In my examples, I use additional, dotted measure lines provided by the editors, Vladimir Morosan and Alexander Ruggieri (1992).
33. Morosan’s 1986 book is an extensive study of Russian pre-revolutionary choral music; it reveals, from a historical (rather than analytical) perspective, Old-Russian origins of much sacred music written at the time.
34. The score (piano reduction only; the choral score is omitted here) and the English translation of the text is given according to Morosan and Ruggieri’s 1992 edition of Rachmaninoff’s Vigil.
35. This introductory C-major chord, on the word Amen, represents a response to a hypothetical preceding statement by the priest. It may or may not be performed at concerts (Morosan and Ruggieri 1992, v).
36. Pairing of second-related keys, though less common than third-related, has been discussed both in English- and Russian-language writings. The latter include Sposobin (1951, 149) and Kholopov (1988, 176), for whom such fluctuation between keys represents a subtype of tonal mutability (as opposed to modal, which does not deal with tonics of keys, but rather with single-tone centers, or ustois).
37. Rhetorically, the final cadence represents a bow that concludes this call for worship. Khannanov (2011, 16–17) describes the ending of the hymn as “cathartic” in the sense that it provokes an extraordinary emotional reaction by “exceeding normative length of syntax and breath.”
38. Johnston (2014) emphasizes the importance of diatonic modes in Rachmaninoff, especially the Phrygian modal idiom. He also acknowledges the potential of this idiom to produce dominant-tonic ambiguities (Johnston 2014, 4.7), which is precisely what happens in the present movement.
39. This sense of an abandoned process sometimes appears in Russian writings on folk and church music. Kholopov (1988, 176) speaks about endings “not on the main center” (ne na glavnom ustoe).
40. The upper part is not a pre-existent chant melody, but Rachmaninoff’s intent to compose a “conscious counterfeit” of Russian chant (Sergei Bertensson and Jay Leyda 1956, 191) justifies a view of the soprano melody as “quasi-chant.”
41. On the auxiliary cadence, see Poundie Burstein 2006.
42. Of course, such a view, based on harmonic functions, is no longer form-based. Instead of viewing certain harmonies as structural based in their formal position, we do so based on their harmonic relationships.
43. The cadence in m. 12 is fundamentally elided, not deceptive, even though it follows a deceptive cadence pattern on the surface—ii⁶–V⁷–vi in C. If one shifts the chant entry in the bass by a half note forward (thus removing the phrase overlap), or shifts it into a different voice, one ends up with a perfectly normal PAC. As Markus Neuwirth (2015) has recently explained, the deceptive cadence proper, at least in eighteenth-century repertoire, does not function as a true cadence, but rather as a strategy of postponing a cadence. This idea was first suggested by Caplin (1998).
44. On the concept of the fifth-divider (Quintteiler), see Heinrich Schenker (2004) and Allen Cadwallader and David Gagné (2016). The possibility of a “normal” Schenkerian reading of the movement results from the fact that the standard tonal progression ii–V–I is (or can be seen as) a partial PH complex.
45. My own intuition is that, in m. 12, the formal boundary is somewhat suppressed, and thus the A-minor harmony gets less emphasis than the other three PH members; it is, in other words, less structural.